樹形図

競プロでよく出題される問題には、「何通りありますか？」「何個・何組ありますか？」といった、数え上げる問題があります。ここでは、簡単な問題を例にして考え方を見ていきます。

基本的な数え上げの方法

「何通りありますか？」というような問題を考える場合、一番基本的な数え方は、「すべて書き出す」方法です。

例えば、「○」と「×」を使って、横一列に3つ並べる方法が何通りあるか考えてみます。「○」も「×」も、いくつ使ってもいいし、使わないものがあってもいいとします。

この場合、数が少ないので、簡単に書き出すことができます。次のようになります。

○○○
　○○×
　○×○
　○××
　×○○
　×○×
　××○
　×××

すべてを書き出して数える方法は確実ですが、漏れやダブりがないようにしなければいけない点に注意します。そのためには、ルールを決めて書き出していくのがいいです。上の例では、左側に○があるほうが上に来るように書き出しています。

書き出す順序にルールを設けて順番に書き出せば、漏れやダブりが起こりにくいです。このように書き出せば、 $8$ 通りであることがわかります。

樹形図

先ほどは、すべて書き出して数えましたが、同じ文字を何度も書くのが少し大変ですね。

たとえば、先ほど書き出した内容をよく見ると、上の4つは、1番左が全部○で、下の4つは1番左が全部×です。これらをまとめて次のように書いてみます。

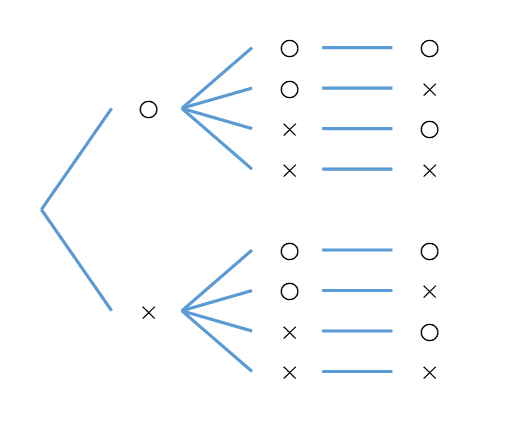
左から2つ目も共通しているものがあるので、まとめてみます。

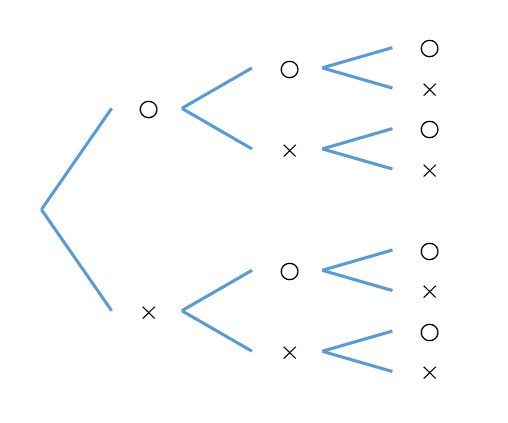
こうすると、共通しているものがまとめられるので、文字を書く量が減っていいですね。これを反時計回りに90度回転すると、地面から木が生えているように見えるので、このような図を樹形図(tree diagram) といいます。

樹形図を用いてすべてのケースを書き出すと、文字を書く量が減るだけではありません。数え方もわかりやすくなります。

上半分と下半分をよく見ると、左から2つ目と3つ目の並び方はまったく同じことがわかります。そのため、並べ方は、

2×（左から2つ目と3つ目の並べ方）

となることがわかります。「2×」というのは、一番左が○のときと×のときの2セットある、ということです。

同じように考えると、左から2つ目と3つ目の並べ方は、左から2つ目の決め方が2通りあって、左から3つ目の決め方も2通りあります。つまり、すべての並べ方は、\[ 2×2×2 \]通りであることがわかります。

樹形図をかけば、同じ構造になっている場所を見つけやすくなり、どのように数えればいいかがわかりやすくなります。左から1つ目、2つ目、3つ目は、それぞれ○か×の2通りあって、これらは互いに無関係に決まるものなので、 $2^3$ 通りだとわかります。

この考え方がわかれば、「3つ並べる」の部分が変わっても、同じように数えられることが分かります。5つ並べるなら $2^5$ 通りだし、10個並べるなら $2^{10}$ 通りです。「 $n$ 個並べる」場合に、どういう答えを出せばいいか、どういうコードを書けばいいかがわかるでしょう。 $n$ が $10$ 以下の正の整数という制約であれば、次のようなコードで求められます（参考：整数の整数乗）。

#include <iostream>
using namespace std;

int main() {
  int n; cin >> n;
  int a = 1;
  for (int i = 0; i < n; i++) a *= 2;
  cout << a;
  return 0;
}

$n$ がもう少し大きい可能性があるなら、 $10^9 + 7$ で割った余りを答えることが多いです。例えば、100個並べるときでも正しい答えを出そうとすると、次のようになります（参考：余りの計算）。

#include <iostream>
using namespace std;

int main() {
  int n; cin >> n;
  long long a = 1, MOD = 1e9 + 7;
  for (int i = 0; i < n; i++) {
    a = (a * 2) % MOD;
  }
  cout << a;

  return 0;
}

例えば、100 を入力すると、976371285 が返ってきます。これは、 $2^{100}$ を $10^9+7$ で割った余りです。

「○, ×」の2種類ではなく、「○, ×, △」というように、3種類の文字を並べる場合も、樹形図がどうなるかを考えれば、数え方がわかるでしょう。線が2つに分かれていた部分が、3つに分かれるように変わり、同じ構造が3つできることがわかります。そのため、「3つ並べる」なら $3^3$ 通りで、10個並べるなら $3^{10}$ 通りとなることがわかります。

ここまでの内容を踏まえると、AtCoder ABC 140 A - Password がわかるでしょう。

積の法則

樹形図をかくと、同じ構造を見つけやすいですね。同じ構造があれば、まとめて数えることができて便利です。先ほどの例であれば、1つ目を決めれば、2つ目・3つ目の決め方は同じ図が続くので、「2×（左から2つ目と3つ目の並べ方）」と掛け算で求められますからね。

このように、同じ構造があれば、掛けて計算できることを、積の法則といいます。少し抽象的に書くと、次のようになります。

上の例では、1つ目の決まり方が2通り、2つ目の決まり方が2通り、3つ目の決まり方が2通りあって、それぞれ独立に決まるので、3つの並べ方は $2\times 2\times 2$ 通りになる、ということです。

簡単な例であればそれほど難しくはない（というか、当たり前に思える）のですが、競プロでの数え上げの問題では頻繁に使う考え方です。

おわりに

ここでは、競プロの数え上げの問題を考えるときに使える、樹形図を紹介しました。簡単な問題では、先ほど紹介した樹形図を使った書き出しが役に立つでしょう。

他にも数え方についてはいくつかの考え方があります。高校生向けのページですが、【導入】数え方の基本 で紹介しています。下にある5つあるリンクのうち、下の3つが該当します。簡単に内容をいうと、「わざとダブらせて数えてから不要なものを引いたり、2重に数えてからあとで2で割ったりする方法」「全体から、不要なものを引く方法」「今数えたいものに関連する、別のわかりやすいものを数える方法」を取り上げています。

なお、樹形図について数学の内容として解説しているページは、【基本】まとめて数えるにあります。