素数とエラトステネスのふるい

ここでは、ある値以下の素数を全部求める、というときに使える、「エラトステネスのふるい」について見ていきます。

素数ふたたび

2以上の整数が素数であるというのは、正の約数が $1$ とそれ自身だけのときをいいます。言い換えると、正の約数が2個のとき、ということです。

なので、ある2以上の整数 $a$ が素数かどうかを判定するには、愚直にやるなら、 $2$ 以上 $a-1$ 以下の整数 $b$ を持ってきて、 $a\div b$ が割り切れるかどうかをチェックします。そのような $b$ がないなら（つまり、 $a$ を割り切るようなものがないなら）、 $a$ は素数だとわかります。もう少し効率的にやるなら、 $\sqrt{a}$ 以下の整数に対してチェックすればいいのでした（参考：素数と合成数）。

ただ、競プロの問題では、ある数が素数かどうかではなく、1000以下の素数を全部求めたい、どれだけあるか数えたい、というようなこともあります（例：AOJ Problem 0009: Prime Number）。まじめにやるなら、次のC++のコードのように、それぞれの数に対して、 $2$ から順番に割り切れるかどうかチェックすることになります。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
  int MAX = 1000, times = 0, cnt = 0;

  for (int i = 2; i <= MAX; i++) {
    bool isPrime = true;
    for (int j = 2; j <= sqrt(i); j++) {
      times++;
      if (i % j == 0) {
        isPrime = false;
        break;
      }
    }
    if (isPrime) {
      cout << i << " ";
      cnt++;
    }
  }
  cout << "\\n" << times << " " << cnt;
  return 0;
}

2 から 1000 までの各数を i に格納しています。 j を 2 から sqrt(i) までの数、つまり $\sqrt{i}$ 以下の整数を持ってきて、割り切れるかどうかをチェックしています。最後まで割り切れなければ素数と判定しています。素数ならその数を表示し、最後に for文を通った回数と素数の個数を表示しています。上のコードを実行すると、内側のfor文を5288回通ったことがわかります。

このように求めることもできますが、素数をまとめて求めたい場合には、以下で説明する「エラトステネスのふるい」と呼ばれる手法を使うことが多いです。

エラトステネスのふるい

引き続き、1000以下の素数を全部求める方法を考えます。このときに、それぞれの数 $a$ に対して、 $2$ から $a-1$ の整数を持ってきて（もしくは $\sqrt{a}$ 以下の整数を持ってきて）割り切れるかどうかチェックするのは、少し非効率です。

というのも、例えば、 $10$ や $24$ などは、 $2$ の倍数だから、すぐに素数ではないとわかります。4以上1000以下の偶数は素数ではないことは明らかなので、チェックする必要はありません。これだけで、調べる数がざっくり半分になります。

また、 $15$ とか $25$ も $5$ の倍数だから、すぐに素数ではないとわかります。これらに対して、「2で割れるかな？」「3で割れるかな？」と調べていくのは無駄です。

このように、素数じゃないとわかっているものは、はじめから除外して考えたほうがよさそうです。調べる数が減って、速く調べ終わることができます。

この考え方を発展させると、ある数が素数だとわかった時点で、それより大きい倍数はすべて除外してもいいことがわかります。その素数に2以上の整数を掛けたものは、どれも合成数になるので、素数かどうかをチェックする必要はありません。

以上のことから、次のような手順で素数を求めます。まず、1000までの数が入る配列を用意し、初期値として0を入れておきます。そして、2から調べていきます。インデックス2には1を入れ、2より大きい2の倍数には、配列に -1 を入れていきます。次に、配列に 0 が入っているものを見つけて 1 を入れ、その値より大きい倍数には -1 を入れていきます。あとはこれの繰り返しです。このようにして、素数には 1 を、合成数には -1 を入れていきます。コードで書くと、次のようになります。

#include <iostream>
using namespace std;

int main() {
  int MAX = 1000, times = 0, cnt = 0;
  int a[MAX + 1] = {};

  for (int i = 2; i <= MAX; i++) {
    if (a[i] == 0) {
      a[i] = 1;
      cnt++;
      for (int j = 2; j <= MAX; j++) {
        times++;
        if (i * j > MAX) break;
        a[i * j] = -1;
      }
    }
  }
  for (int i = 2; i <= MAX; i++) {
    if (a[i] != -1) cout << i << " ";
  }
  cout << "\\n" << times << " " << cnt;
  return 0;
}

i = 2 の場合、2 * 2 や 2 * 3 などの、2以外の2の倍数のインデックスには、-1 がセットされます。そのため、a[3] は 0 が入ったままなので、これより小さい数の倍数にはなっていない、つまり、素数であることがわかります。

続いて、3以外の3の倍数のインデックスには-1をセットします。こうしたとき、a[4] はi = 2のときに -1 をセットしたので、素数ではないことがわかります（4の倍数は2の倍数を消したときにすでに消えています）。なので、次は 5 です。以降、繰り返し実行していくと、 $i$ が素数なら a[i] は 1 で、素数でないなら -1 となります。更新されていく様子をまとめると、次のような図になります。

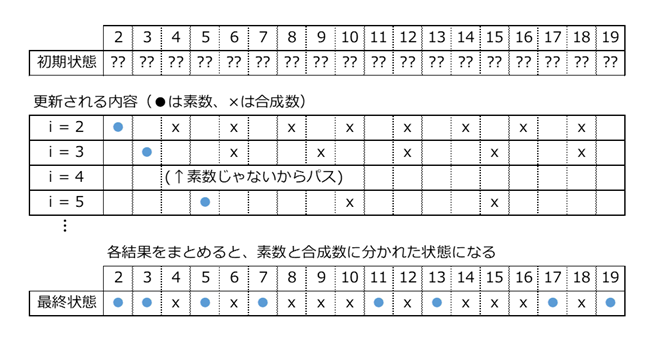
上のコードでは、for文を実行した回数が最後に表示されます。2126回となり、はじめに書いたコードよりだいぶ回数が減りました。ここでは 1000以下の素数を調べただけですが、もっとたくさんの素数を一気に調べたい場合は、計算回数の差はどんどん広がります。後者のやり方では、数が大きくなるほど「素数じゃないもの」が増え、パスしていいものが多くなっていくことから、より速く計算できることは想像できると思います。

もし素数だけの集合が欲しいなら、素数だと判明したものから順番に vector に push_back していくといいでしょう。

素数かどうかを判定していくには、素直にやる場合は「正の約数は2個だけかな？」と調べていくことになりますが、エラトステネスのふるいでは、「正の約数を3個以上持つものを片っ端から潰していく」ことで計算回数を減らしています。

コードを見直す

エラトステネスのふるいを使った先ほどのコードを見直してみましょう。

実は、素数に 1 をセットする意味はありません。 -1 が入っているなら合成数とわかるし、初期値である 0 なら素数だと判断できます。なので、 1 をセットする処理は削ります。

また、素数かどうかを調べるのは、MAX までではなく、sqrt(MAX) までで構いません。sqrt(MAX) 以降は、合成数なら sqrt(MAX) 以下の整数で割り切れているはず（参考：素数と合成数）なので、すでに素数かどうかは確定しているからです。

こうすると、素数の個数を調べる処理も変える必要があります。sqrt(MAX) より後を調べないため、「合成数とわかったら除外していく」という数え方に変えます。コードは次のようになります。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
  int MAX = 1000, times = 0, cnt = MAX - 1;
  int a[MAX + 1] = {};

  for (int i = 2; i <= sqrt(MAX); i++) {
    if (a[i] == 0) {
      for (int j = 2; j <= MAX; j++) {
        times++;
        if (i * j > MAX) break;
        if (a[i * j] == 0) cnt--;
        a[i * j] = -1;
      }
    }
  }
  for (int i = 2; i <= MAX; i++) {
    if (a[i] != -1) cout << i << " ";
  }
  cout << "\\n" << times << " " << cnt;
  return 0;
}

実行すると、計算回数がさらに減ったことがわかります。まだ工夫の余地はありますが、おおまかな方針は上のようになります。

ここまでの内容を踏まえると、AOJ ALDS1_1_C Prime Numbers や AOJ Problem 0009: Prime Number に挑戦できるかもしれません。計算時間を考えないといけないので少し難易度が高くなりますが、頑張ってみましょう。

おわりに

ここでは、一度に素数を求める、エラトステネスのふるいと呼ばれる方法を見てきました。「該当しないものをどんどん消していく」というこの手法を使えば、素数の一覧を効率よく見つけることができます。ちなみに、エラトステネスは、紀元前3世紀ごろの学者です。こんなに昔から知られていた手法なんですね。