🕒 2019/10/15 🔄 2024/10/16

素数と合成数

🎵

ここでは、整数の問題でよく出てくる素数について見ていきます。

📘 目次

素数と合成数

2以上の整数について、正の約数が $1$ とその数だけであるようなとき、その数を素数といいます。また、素数でない2以上の整数は、合成数といいます。たとえば、 $2$ や $3$ や $5$ は、 $1$ とその数だけが正の約数なので、いずれも素数です。一方、 $4$ や $6$ は、 $1$ とその数以外に、 $2$ も約数となるので、合成数です。 $0$ や $1$ は、素数でも合成数でもありません。

素数とは、「正の約数の個数が2個だけの正の整数」と言い換えることもできます。

競プロでは、ある整数 $N$ に対して、それが素数かどうかを判定する場面があります。いくつか方法はありますが、愚直にやるなら次のようになります。 $2$ から $N-1$ の中で、 $N$ の約数になっているものを探します。そんな約数が見つかれば合成数、見つからなければ素数です。

これを踏まえれば、AtCoder ARC 017 A - 素数、コンテスト、素数に取り組めるでしょう。

素数の判定を改善する

2以上の整数 $N$ が素数であるとは、正の約数が $1$ と $N$ だけであるときを言います。そのため、素数であることをチェックするには、 $2$ から $N-1$ までの整数の中で、 $N$ の約数になっているものがないことを調べればいいです。これをそのまま実行すれば、だいたい $N$ 回くらいのチェックが必要となります。

しかし、実はチェックする回数はもっと少なくてすみます。約数のところで見た内容とほとんど同じ（参考：倍数と約数）ですが、ここでもう一度見ることにしましょう。

$17$ が素数であるかどうかをチェックすることを考えましょう。 $2$ が $17$ の約数かどうかは、次のような図を見るとわかります。

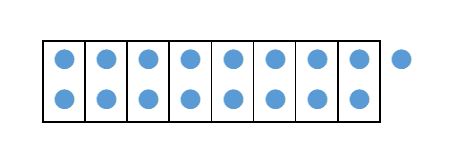
17個の丸を並べます。縦に2個並べたものを1セットにして横に並べていきます。そうすると、8列だと丸が余り、9列だと足りなくなるので、割り切れないことがわかります。

同様にして、縦に3個、4個、5個を並べたときを考えてみましょう。

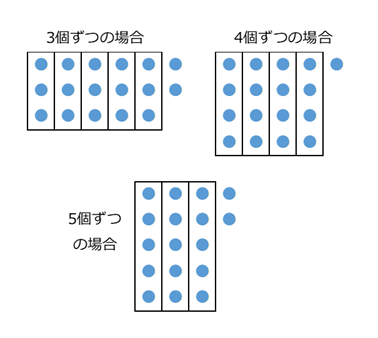
上の図から、どの場合も縦にびっしりと余りなく並べるのは無理なことがわかります。この先も同じようにチェックしていってもいいのですが、実はもうここで終わってしまっても問題はありません。その理由を知るために、最後のケース、縦に5個並べたときを見てみましょう。

すべてが埋まっているわけではないですが、横は4列です。これがすべて埋まっていれば、 $5\times 4$ となるわけですが、もしそうなっているなら、縦に4個並べたときに、 $4\times 5$ という形ですでに出てきているはずです。つまり、縦のほうが長くなっても割り切れるものが見つからなければ、もうそれ以上チェックをしても意味がないことがわかります。

チェックしなければいけないギリギリのラインは、縦と横が同じ数のときです。 $4\times 4=16$, $5\times 5=25$ なので、ちょうど $17$ となることはないですが、縦と横が $5$ のときは $17$ を超えてしまうため、これより先は（余りなく並べられたとしても）縦の方が長いケースしか出てこないことがわかります。

約数のときも、縦が横以下の場合だけを考えればよかったですね（参考：倍数と約数）。素数であることは、正の約数が2個だけと言い換えることもできるので、約数を探すときと似たような考え方を使うことができます。

これを踏まえると、次のようなコードで素数かどうかを確認できます。C++で、 $2$ 以上のint型の整数が入力されたとき、素数なら Yes と返し、素数でないなら例として約数を1つと No を返すコードです。

#include <iostream>
using namespace std;

int main() {
  int a; cin >> a;

  for (int i = 2; i * i <= a; i++) {
    if (a % i == 0) {
      cout << i << "\\n";
      cout << "No\\n";
      return 0;
    }
  }
  cout << "Yes\\n";
  return 0;
}

競プロの問題でよく使われる素数 1000000007, 1000000009, 998244353 や、合成数などを試してみましょう。 $2$ 以上の int 型なら正しく判定されます。

平方根

約数を列挙するコードや上で見た素数を判定するコードでは、次のように書いている部分がありました。

for (int i = 2; i * i <= a; i++) {

先ほどのように $a$ 個の丸を並べるとすると、縦が横以下になるときだけを考えればいいのでした。その境い目が、縦と横の積が $a$ 以下か $a$ より大きいか、でした。その判定をしている箇所が i * i <= a ですが、ここは別のかき方ができます。

2乗して $a$ になる正の数を $a$ の平方根(square root) といいます。数学の世界では、 $\sqrt{a}$ と書いて、「ルート $a$ 」と読みます。例えば、 $\sqrt{4}$ は、2乗して $4$ になる正の数を表すので、 $\sqrt{4}=2$ です。 $\sqrt{100}$ なら、 $10^2=100$ なので、 $\sqrt{100}=10$ となります。

平方根は整数になるとは限りません。例えば、 $\sqrt{17}$ は、2乗してちょうど $17$ になる整数がないので、この値は整数ではありません。しかし、だいたいの大きさはわかります。 $4^2=16$, $5^2=25$ なので、$4$ と $5$ の間にある数です。

今の場合、正確な値を知る必要はありません。正の整数 $a$ の約数を調べたり、これが素数であるかどうかを調べるには、 $\sqrt{a}$ 以下の値を調べばよく、そのためにどの範囲の整数を調べればいいかがわかればそれで十分です。 $\sqrt{a}$ は2回掛けると $a$ になるので、先ほどのfor文にある $i\times i\leqq a$ という条件は $i\leqq \sqrt{a}$ と同じ内容となります。

C++では、a の平方根を取得するには、sqrt(a) とかきます。cmathのincludeも必要です。これらを使うと、素数かどうかを判定する先ほどのコードは、次のように書き換えることができます。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
  int a; cin >> a;

  // for (int i = 2; i * i <= a; i++) {
  for (int i = 2; i <= sqrt(a); i++) {
    if (a % i == 0) {
      cout << i << "\\n";
      cout << "No\\n";
      return 0;
    }
  }
  cout << "Yes\\n";
  return 0;
}

先ほどと同じように、 $2$ 以上の int 型の値をいろいろと試してみましょう。

素数の性質

素数にはいろいろな性質がありますが、ここでは今後もよく使う基本的な性質を一つだけ紹介しておきます。

その性質とは、「整数 $a,b$ の積が素数 $p$ の倍数なら、 $a,b$ の少なくとも一方は $p$ の倍数」という性質です。例えば、 $ab$ が $13$ の倍数なら、 $a,b$ の少なくともどちらかは $13$ の倍数、ということです。

イメージとしては、 $ab$ が素数 $p$ の倍数とすると、 $a,b$ のそれぞれに $p$ で割り切れる "成分" のようなものが入っていて、それらが掛け合わさった結果 $p$ で割れるようになる、と考えられます。しかし、 $p$ の正の約数は $1$ と $p$ しかないので、どちらかに $p$ がそのまま入っている場合しかない、つまり、少なくともどちらかが $p$ で割り切れる場合しかない、という感じです。

$p$ が素数でない場合は、同じことが成り立つとは限りません。例えば、 $a=4,b=3$ で $p=6$ とすると、 $ab=12$ は $p$ で割れますが、 $a,b$ はどちらも $p$ の倍数ではありません。 $a$ が偶数、 $b$ が $3$ の倍数になっているため、積は $6$ の倍数となりますが、それぞれは $6$ の倍数ではありません。

この素数の性質は、整数に関する計算を何度もやっていると、成り立つことは当たり前のように感じますが、実際に証明するのは大変です。ここでは証明はしませんが、素数や整数の性質を見ていく上では重要な性質で、これから何度も登場します。

おわりに

ここでは、素数の定義と、素数であることを調べる方法について見てきました。 $N$ が素数であるかどうかをチェックするには $\sqrt{N}$ 回くらいのチェックで確かめることができます。この平方根も覚えておきましょう。