素因数分解と約数と倍数

ここでは、素因数分解を行うと、約数や倍数についての情報がわかりやすくなる、ということを見ていきます。具体的な小さな値での例に見た後に、一般的な形でまとめて、最後にコードにしていきます。

素因数分解と約数

ある数が $60$ の約数であるかどうかを考えてみます。

例えば、 $2,3,4,5,6$ は $60$ の約数ですが、 $7,8,9$ は $60$ の約数ではありません。 $10,12,15$ は約数で、 $11,13,14$ は約数ではありません。なんだかきれいな法則はないように見えますね。

しかし、素因数分解を使ってみると、約数かどうかを判定するのはわかりやすくなります。 $60$ を素因数分解すると\[ 60=2^2\times 3\times 5 \]となります。上で見た約数もいくつか素因数分解してみると、 $2=2$, $4=2^2$, $6=2\times 3$, $10=2\times 5$, $12=2^2\times 3$ となります。約数の素因数は、どれも $60$ の素因数のどれかになっていますね。一方、 $7,11,13,14$ などの例を見ると、 $60$ の素因数でないものを含んでいる場合は、約数にはなっていません。

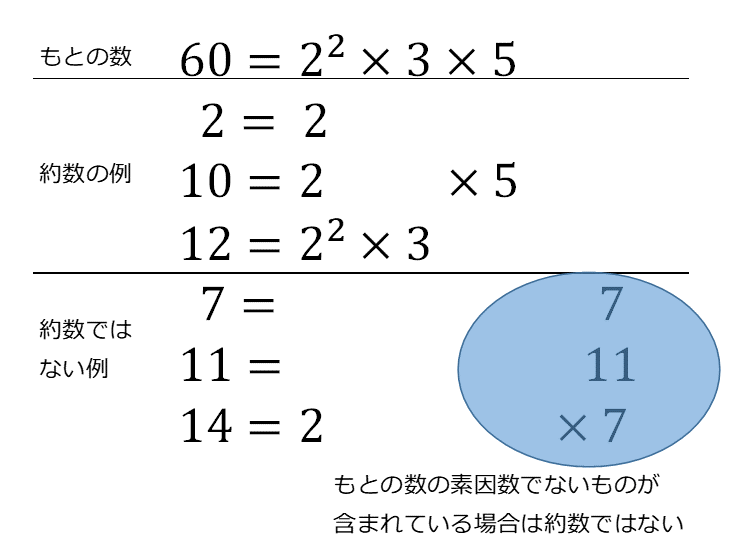
例えば、 $60$ が素数 $7$ で割り切れるなら、どれかの素因数が $7$ で割れないといけません（参考：素数と合成数#素数の性質）が、そんなことは起こりません。なので、 $2,3,5$ 以外の素因数を含むものは約数にはなりません。

次に、素因数の指数（右上にある数）に注目してみましょう。 $60$ を素因数分解したとき、素因数 $2$ の指数は $2$ となっています。約数のほうは、素因数 $2$ の指数は2以下となっています。一方、約数ではない例に挙がっている $8$ は $2^3$ と素因数分解できるので、指数は3です。つまり、素因数の指数が超えてしまった場合は、約数になっていません。

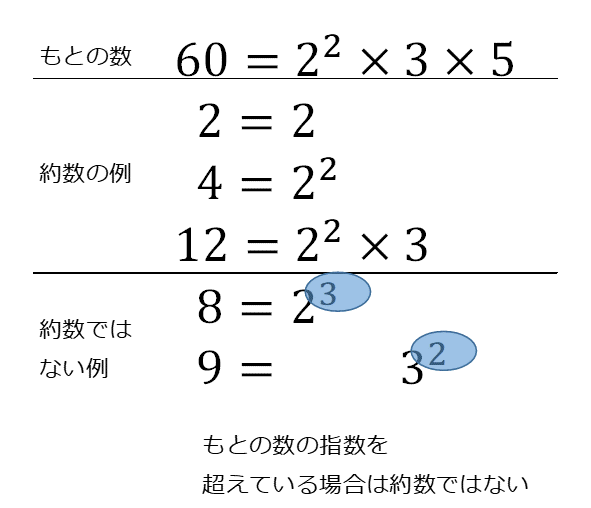
例えば、 $60$ が $2^3$ で割れるなら、 $2$ で3回割れないといけませんが、 2回割ったあとは $3\times 5$ となり、これ以上 $2$ では割れません。そのため、指数が元の数を超えていれば約数にはなりません。一方、 $2\times 3$ のように、どの素因数に対しても指数が元の数のもの以下となっていれば、\[ 2^2\times 3\times 5 = (2\times 3)\times(2\times 5) \]というように分解できるので、約数であることがわかります。

以上のことをまとめてみます。ある正の整数 $a$ が $60=2^2\times 3\times5$ の約数になっているかどうかを考えます。もし $a$ が $2,3,5$ 以外の素因数を含んでいたら、約数ではありません。また、各素因数の指数をみたとき、 $60$ を素因数分解したときより大きいものがあれば、約数ではありません。それ以外なら、約数となります。

つまり、素因数分解の形がわかっていれば、素因数とその指数を見比べるだけで約数かどうかがわかるということです。

素因数分解と倍数

素因数分解をすると、倍数についての情報もわかりやすくなる、ということを見ていきます。これは、「 $a$ が $b$ の倍数」と「 $b$ が $a$ の約数」とが同じ意味であることから、先ほどの約数の話を逆に用いればいいことがわかります。

例えば、素因数分解後の形で、 $2^3\times 3\times 5^2$ が $2^2 \times 3$ の倍数になっているかどうかを考えましょう。 $2^3\times 3\times 5^2$ が $2^2 \times 3$ で割り切れるかを考えればよく、約数のときと同じようにすれば、素因数と指数を調べればいいことがわかります。素因数 $2$ の指数は $2$ で、素因数 $3$ の指数は $1$ だから、 $2^3\times 3\times 5^2$ の各素因数と比べて、指数が同じか小さいため、割り切れることがわかります。なので、 $2^3\times 3\times 5^2$ は $2^2 \times 3$ の倍数です。

一方、 $2^3\times 7^2$ が $2^2 \times 3$ の倍数かどうかも同様に考えると、 $2^3\times 7^2$ は $2$ の指数が $2$ 以上ですが、素因数 $3$ を含んでいません。そのため、 $2^2 \times 3$ の倍数ではありません。

素因数分解の形がわかっていれば、素因数とその指数を見比べるだけで倍数かどうかがわかります。

一般的なまとめ

ここまでの内容からもわかるとおり、素因数分解をした結果、各素因数の指数を比べると、約数や倍数の判定ができることがわかります。

2つの正の整数 $A, B$ を素因数分解したときにあらわれる素因数を全部集めたとします。素因数が $n$ 種類あるとして、 $p_1,p_2,\cdots, p_n$ と書くことにしましょう。 $A,B$ の素因数 $p_i$ の指数を $a_i, b_i$ で表すことにします（片方が正で片方が0のケースもある。両方0のケースは除く）。つまり、
\begin{eqnarray}
A &=& p_1^{a_1}p_2^{a_2}\cdots p_n^{a_n} \\[5pt]
B &=& p_1^{b_1}p_2^{b_2}\cdots p_n^{b_n}
\end{eqnarray}と表したとします。このとき、すべての $i$ について、 $a_i \geqq b_i$ なら、 $A$ は $B$ の倍数であり、 $B$ は $A$ の約数であることがわかります。 $a_i \gt b_i$ となるケースと $a_j \lt b_j$ となるケースが混在する場合は、約数にも倍数にもなりません。

コードで表現する

一般的には、約数や倍数であるかどうかは、割り切れるかどうかをチェックすればよく、素因数分解をするほうが大変です。そのため、約数や倍数であることを調べるためにわざわざ素因数分解を使うケースは少ないのですが、今後、競プロで整数問題を解くにあたって、この考え方が使える場面はあります（例えば、近々説明する約数の個数とか公約数とか公倍数とか）。ですので、最後に、素因数分解に着目した、約数・倍数の判定用コードを考えてみましょう。

2つの正の整数 $a,b$ に対して、 $a$ が $b$ の約数であるかどうかを考えます。先ほども見た通り、 $a$ が $b$ の約数であれば、各素因数について、指数は $a$ のものが $b$ のもの以下となるはずです。これを確かめましょう。

まず、 $2$ から $\sqrt{a}$ 以下の整数に対して、 $a$ を割り切るかどうかをチェックします。もし割り切れる場合は、割り切れなくなるまで割ってみます。同じ以上の回数で $b$ も割り切れるかどうかをチェックします。割り切れないなら、約数ではないことがその時点で分かります。これを繰り返していきます。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
  int a, b; cin >> a >> b;

  for (int i = 2; i <= sqrt(a); i++) {
    while (a % i == 0) {
      if (b % i != 0) {
        cout << i << "\\nNo";
        return 0;
      }
      a /= i;
      b /= i;
    }
    if (a == 1) break;
  }

  if (a != 1 && b % a != 0) {
    cout << a << "\\nNo";
  } else {
    cout << "Yes";
  }
  return 0;
}

上のコードでは、 a が b の約数なら Yes と返し、約数ではないなら、どの素因数で問題があったかを返した後に No を返すようにしています。

sqrt(a) 以下の値を調べていくので、最後に a a に素数が1つ残るケースがあります（参考：素因数分解）。この場合を最後に調べています。

おわりに

ここでは、素因数分解の結果を利用することで、約数や倍数であることを簡単に判定できることを見ました。整数の問題ではここで見た考え方が利用できる場面も出てきます。