🕒 2019/11/13 🔄 2024/10/16

順列

🏈

ここでは、異なるものを1列に並べる方法を数えていきます。

📘 目次

順列

競プロの問題では、$1$ から $N$ までの $N$ 個の整数を並び替える、という状況がよく出てきます（例：AtCoder ABC 135 B - 0 or 1 Swap）。

このように、異なるものを1列に並べたものを順列(permutation) といいます。例えば、次の問題文 AtCoder ARC 032 D - Rotation Sort の最初にも出てきています。

競プロでは、順列に対して何かをする、というケースが多いのですが、ここでは、まずはこのような並べ方が何通りあるかを考えましょう。

例として、 $1$ から $4$ までの数字を並び替えて一列に並べるとしましょう。樹形図をかいてすべて書き出すと、次のようになります。

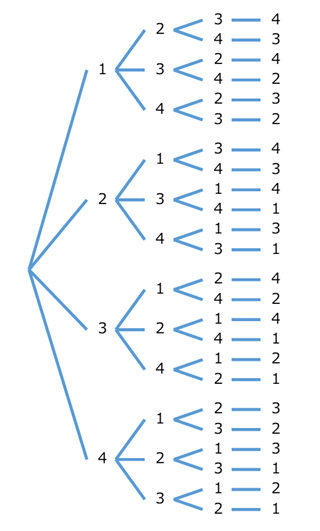
こうすると、同じ構造のブロックが4つあることがわかります。樹形図の時とは異なり、2つ目以降に並んでいるものは違いますが、樹形図の構造（枝が何本あるか）は同じです。また、各ブロックは、さらに3つのパーツに分かれています。下の図を見ると、緑の部分が4つあり、黒線で囲ったところが3つあることがわかります。

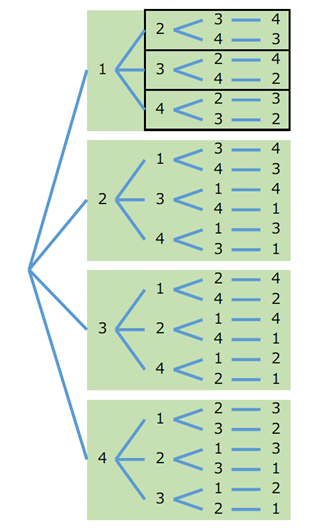
黒線の中はさらに2つの枝にわかれています。そのあとは残りの1つが確定します。同じ構造の部分はまとめて計算できることから、並べ方は、\[ 4\times 3\times 2\times 1 \]から、24通りだと計算することができます。

見方を変えると、4つあったブロックは、一番左に何を置くかが4通りあることに対応しています。1つ並べると残りは3つあるので、左から2番目に何を置くかは3通りありますが、これが黒線の3つの箱に対応しています。残り2つを並べるには、○□と並べるか□○と並べるかの2通りです。このように、左から順番に並べたときに、各場所に置くものが何通りあるかを考えることで、並べる方法を数えることもできます。こうして\[ 4\times 3\times 2\times 1 \]通りと計算することができます。

同じように考えると、 $N$ 個の異なるものを1列に並べる場合、並べる方法の総数は、 $1$ から $N$ までをすべて掛け合わせたものになります。この値を $N$ の階乗といい、 $N!$ という記号で表します。つまり、\[ N!=N(N-1)(N-2)\cdots 2\cdot 1 \]ということです。先ほどの例から、 $1$ から $4$ までを並べる方法は、 $4!$ 通りである、と表すことができます。

階乗を求める方法は、和や階乗と再帰関数で見ているので、参考にしてみましょう。

すべての順列を列挙する

C++では、順列を列挙するのに便利な、next_permutation が用意されています（ほかの言語でも似たものがあるかもしれません）。これは、次の順列を返してくれるものです。

例えば、 1, 2, 3, 4 を並び替えたものを列挙したい場合は、次のようにするといいです。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
  int n = 1;
  vector<int> v = {1, 2, 3, 4};
  do {
    cout << n++ << ":";
    for (int i = 0; i < v.size(); i++) {
      cout << " " << v[i];
    }
    cout << "\\n";
  } while (next_permutation(v.begin(), v.end()));
  return 0;
}

これを実行すると、並び替えたものが順番に表示されていきます。先ほどの樹形図と同じように、小さいものが左にあるものほど先に出てくる、という順番で出てきます。4桁の数字だと考えると、小さい順から出てくるとも言えます。

比較する順序は自分で好きなように指定することもできます。次のようにインデックスのほうを並び替えるようにすればいいです。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
  int n = 1;
  vector<int> v = {0, 1, 2, 3, 4};
  vector<char> words = {'a', 'i', 'u', 'e', 'o'};
  do {
    cout << n++ << ": ";
    for (int i = 0; i < v.size(); i++) {
      cout << words[v[i]];
    }
    cout << "\\n";
  } while (next_permutation(v.begin(), v.end()));
  return 0;
}

words に対して、直接 next_permutation を使うと、アルファベット順になってしまいます。しかし、上のようにすれば、仮名表記にした場合にアイウエオ順に現れるようになります。

実行してみるとわかりますが、4つのものを並び替える方法が全部で24通りであるのに対し、5つのものは120通りもあります。並べ方の総数はすぐに大きくなり、 $13!$ の時点で int 型を超えてしまいます。そのため、並び替えを直接実行して解く競プロの問題は少ないですが、総数をどのように求めるか、どのような式になるかを理解しておくことは、他の数え上げの問題を解くときにも役立つでしょう。

順列を使わなくてもできますが、AtCoder ARC 013 A - 梱包できるかな？の問題のように、全パターンを試すような問題で利用することができます。また、これも順列を使わなくてもできますが、AtCoder ABC 054 C - One-stroke Path のような $N$ が小さい問題では、全部列挙して考えることもできます。

一部だけ並べる

ここまでは、異なる $n$ 個のものをすべて使って一列に並べる場合の数を見ました。ここでは、全部ではなく、一部だけを並べることを考えます。

例えば、a, i, u, e, o の5つから異なるものを3つ選んで一列に並べるとしましょう。1文字目の決め方は5通りで、次に2文字目を決める方法は4通りです。続いて3文字目は3通りだから、 $5\times 4\times 3$ 通りとなります。樹形図を3段階目までをかく、と考えて同じ構造の部分をまとめて数える、という方法でも同じ式にたどりつけるでしょう。

一般に、異なる $n$ 個のものから $k$ 個選んで一列に並べる方法の総数は\[ n\cdot(n-1)\cdots(n-k+1) \]となります。この値もよく使うので、次のような記号で表します： ${}_n \mathrm{P}_k$ 。

冒頭で見たように、異なる $n$ 個のものをすべて使って一列に並べる方法の総数は $n!$ 通りだったので、 ${}_n \mathrm{P}_n=n!$ が成り立ちます。

また、 ${}_n \mathrm{P}_k$ は、 $n$ までの積から $k$ までの積を除いたものと考えることもできるので、\[ {}_n \mathrm{P}_k=\dfrac{n!}{k!} \]と表すことができます。この表記は、後で見る「組合せ」の問題でも使えるので覚えておくと役立つでしょう。

おわりに

ここでは、順列の総数について見てきました。樹形図をもとに考えると、どのように計算すべきか理解しやすくなるでしょう。

数学の内容として学びたい場合は、【基本】順列やこの関連ページが参考になるでしょう。