🕒 2019/11/20 🔄 2024/10/16

パスカルの三角形と組合せ

😜

ここでは、2方向に進む最短経路の総数を使いながら、 ${}_{n}\mathrm{C}_k$ に関する性質を見ていきます。また、パスカルの三角形についても見ていきます。

📘 目次

最短経路、右を選ぶか上を選ぶか

最短経路の総数（二方向の場合）では、次のような図で2方向に進む最短経路の総数を求める方法を見ました。

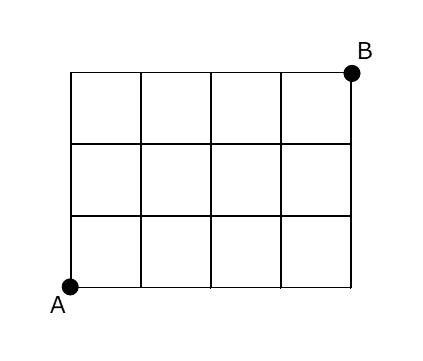
左下の点から、右に $m$ 、上に $n$ だけ移動した点に行く最短経路の総数は、 $m+n$ 回の移動のうち、右に移動する $m$ 回を選ぶ方法の総数と同じなので、 ${}_{m+n}\mathrm{C}_m$ 通りだと計算できます。

右に移動する $m$ 回を決めれば、残りは上に移動することが決まり、経路が定まります。もちろん、右への移動ではなく、上への移動を先に決めても構いません。上に移動する $n$ 回を決めれば、残りは右に移動することが決まるので、この方法でも経路を決めることができます。つまり、最短経路の総数は、 ${}_{m+n}\mathrm{C}_n$ 通りと書くこともできます。

一般に、次の式が成り立ちます。\[ {}{m+n}\mathrm{C}_m = {}{m+n}\mathrm{C}_n \]

階乗を使った式で書けば、どちらも $\dfrac{(m+n)!}{m!n!}$ となることからも、両者が等しくなることがわかります。

最短経路、左から行くか下から行くか

最短経路の総数（二方向の場合）で、先ほど見た方法とは別に、左からくる経路と下からくる経路に分けて数えていく方法も見ました。

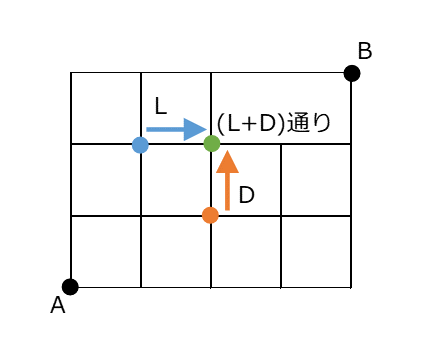
右に i 、上に j 移動した点へいく最短経路の数を dp[i][j] で表すとします。i, j が正の整数の場合、左からくる経路の数は dp[i - 1][j] であり、下からくる経路の数は dp[i][j - 1] と表すことができます。この2つのケース以外はないので、よって次の式が成り立ちます。

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

ただ、例外的なケースがあります。まず、dp[0][0] = 1 です。また、i, j が 0 の時は dp[i - 1][j] や dp[i][j - 1] は 0 として計算します。

これらの例外を加味して、上の漸化式を使って更新していくと、各点への最短経路の総数が順番に計算できます。

dp[m][n] は、右に m 、上に n 移動した点へいく最短経路の数なので、 ${}{m+n}\mathrm{C}_m$ と一致します。また、dp[m - 1][n], dp[m][n - 1] もそれぞれ書き直すと、 ${}{m+n-1}\mathrm{C}{m - 1}$, ${}{m+n-1}\mathrm{C}m$ と表すことができます。よって、この漸化式を、 $\mathrm{C}$ を用いて書くと、次のようになります。\[ {}{m+n}\mathrm{C}m = {}{m+n-1}\mathrm{C}{m-1} + {}{m+n}\mathrm{C}_m \]これも、組合せに関連する式としては重要なものです。競プロでは、組合せの総数を求めるために必要な漸化式として使います。

パスカルの三角形

ここまでの内容を踏まえて、各点への最短経路の総数を書き足してみます。実際の総数を書けば、次のようになります。

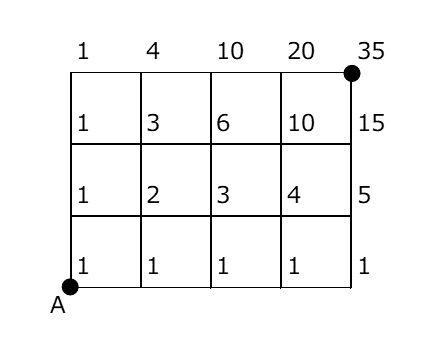
これを回転して、左下の点が一番上にくるようにし、次の段には1回の移動で移れる点、次の段には2回の移動で移れる点、…、となるようにしてみます。
\begin{array}{ccccccccccc}
&&&&& 1 &&&&&\\[5pt]
&&&& 1 && 1 &&&&\\[5pt]
&&& 1 && 2 && 1 &&&\\[5pt]
&& 1 && 3 && 3 && 1 &&\\[5pt]
& 1 && 4 && 6 && 4 && 1 &\\[5pt]
1 && 5 && 10 && 10 && 5 && 1\\[5pt]
\end{array}

上から $n$ 段目、左から $k$ 番目の数字（ただし最初を0段目・0番目とする）は、元の最短経路を考えていた図で考えれば、右へ $k$ 回、上へ $n-k$ 回移動した点への最短経路の総数を表しているので、 ${}_{n}\mathrm{C}_k$ とも書けます。

先ほどの漸化式からもわかりますが、それぞれの数は、左上の数字と右上の数字を足したものになっています。例えば、一番下の段にある左側の 10 は、その左上の 4 と右上の 6 の和になっています。他の数字も、このルールを満たしています。

このルールを使い続ければ、下へ下へと大きな三角形を作っていくことができます。これをパスカルの三角形(Pascal's triangle) と呼びます。

パスカルの三角形をよく見れば、AtCoder CODE FESTIVAL 2014 決勝 D - パスカルの三角形も解くことができるでしょう。

パスカルの三角形を見ながら、 ${}{n}\mathrm{C}_k$ を求めるコードを書いてみます。最短経路の総数（二方向の場合）でも見た内容ですが、書き方を少し変えています。リンク先では ${}{m+n}\mathrm{C}_m$ を計算していますが、ここでは、 ${}_n\mathrm{C}_k$ を返すようにしています。パスカルの三角形で、左上の数字と右上の数字を足して求められることをコードにしています。また、 $10^9+7$ で割った余りを返すようにしています。

#include <iostream>
#include <vector>
using namespace std;

int main() {
  long long MOD = 1e9 + 7;
  int n, k;
  cin >> n >> k;
  vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));

  for(int i = 0; i <= n; i++) {
    dp[i][0] = 1;
    for(int j = 1; j <= i; j++) {
      dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % MOD;
    }
  }
  cout << dp[n][k];
  return 0;
}

dp[i][j] は、パスカルの三角形の上から i 段目、左から j 番目の数字に対応しています（最初を0番目と数えています）。dp[i - 1][j - 1] は左上の数字を表しています。j - 1 が負になってはいけないので、0のときだけ特別扱いをしています。dp[i - 1][j] は右上の数字を表していますが、数字がなければ自動的に0が入ります。こうして、パスカルの三角形に出てくる数字を、上から順番に求められます。

競プロでは、n が10000程度であれば、この方法で ${}_n\mathrm{C}_k$ を求めることができます。

なお、前半で見た組合せの性質を ${}n\mathrm{C}_k$ で書くと、
\begin{eqnarray}
{}_n\mathrm{C}_k &=& {}_n\mathrm{C}{n-k} \\[5pt]
{}n\mathrm{C}_k &=& {}{n-1}\mathrm{C}{k-1}+{}{n-1}\mathrm{C}_k \\[5pt]
\end{eqnarray}となります。

おわりに

ここでは、パスカルの三角形を用いて、組合せの性質や、組合せの総数を求める方法を見てきました。競プロの問題では、漸化式を用いて組合せの総数を求めることができることが大事です。組合せの問題に持ち込んで、 ${}_n\mathrm{C}_k$ を計算する場面はよく出てきます。