最短経路の総数（二方向の場合）

ここでは、2方向だけに進める場合の、最短経路を求める問題を考えます。

2方向だけに進める場合の最短経路問題

競プロでは、いろいろなタイプの最短経路問題があります。ここでは、その中でも、2方向だけに進めるという一番シンプルな条件で、最短経路の総数を求める問題を考えてみます。

次のような図を考えます。

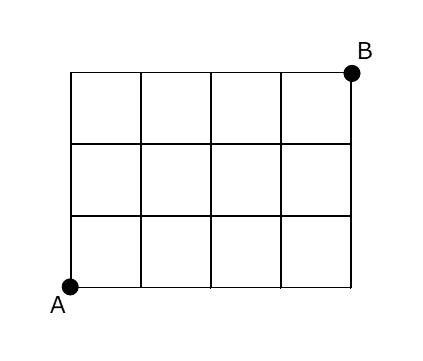
今、左下の点A にいるとします。この点から、線の上をたどって右上の点B に移動する最短経路の数を数えてみましょう。

左や下に行くとゴールから遠ざかってしまうので、最短で行くには上か右だけに移動するしかありません。そんなに大きくない図ですが、いくつか試してみると、移動する方法は結構ありそうです。

実は、この最短経路を数えるのに、組合せ の考え方を用いることができます。自力で思いつくのは難しいですが、どのように応用すれば少し考えてみましょう。

移動の仕方に着目する

先ほどの最短経路の問題を考えましょう。いろいろな経路が考えられますが、どんな経路でも"あるもの"が一定です。

それは、移動の回数 です。上と右にしか行けず、下や左には移動できないので、移動のどこかで3回上に移動し、4回右に移動するしかありません。そして、移動の合計回数は7回となります。

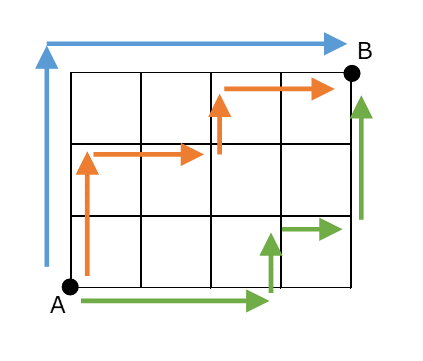
試しに、上の図の青い経路でどのように移動しているかを書いてみると、↑↑↑→→→→となります。また、オレンジの経路は、↑↑→→↑→→となります。緑は、→→→↑→↑↑です。確かに7回移動し、3回は↑、4回は→の移動です。

逆に、↑３つと→４つを並び替えて移動方法を作れば、それに応じて移動の仕方が決まります。

つまり、移動経路と「↑3つ、→4つの並び替え」は、1対1に対応することがわかります。「↑3つと→4つの並び替え」は、「7回の移動のうち、右に移動する4回をどのように選ぶか」と考えることができます。組合せ の後半の「同じものを含んだ順列」で見た考え方です。こうして、最短経路の総数は、${}_7 \mathrm{C}_4=35$ 通りだと求めることができます。

一般に、上と右の2方向だけに動く場合、点 $(0,0)$ から 点 $(m,n)$ に移動する（ $m,n$ は0以上の整数）方法の総数は、 ${}{m+n} \mathrm{C}_m$ 通り、となります。上か右に移動する回数が全部で $m+n$ 回で、そのうち右に移動する $m$ 回をいつにするか選ぶ、と考えています。 ${}{m+n} \mathrm{C}_m$ は、 $m, n$ が小さければ、組合せ で見たように、階乗を計算するコードを使って求めることができます。

各点に注目する

引き続き、2方向だけに動く場合の最短経路の総数について考えます。もう一つの考え方として、各点に注目する、という方法があります。

いきなり点B に行く場合ではなく、点A のすぐ右隣りの分岐点を考えてみます。この点までの最短経路の総数は、もちろん1通りです。点A から右へ1回移動する経路しかないからですね。同様に、点A のすぐ上の分岐点への最短経路も1通りです。

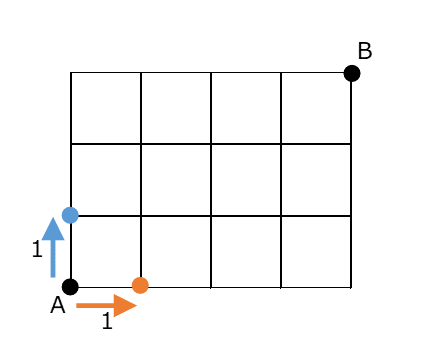
オレンジの点へも1通り、青の点へも1通りです。では、オレンジの点の1つ上（＝青の点の1つ右）にある分岐点への最短経路の総数はどうなるでしょうか。ここに来るには、下から来るか左から来るかの2パターンしかなく、下の分岐点から来る方法が1通り、左の分岐点から来る方法が1通りなので、合わせて2通りだとわかります。

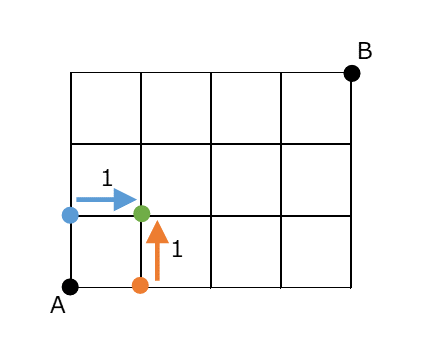
そのさらに上の分岐点はどうなるでしょうか。これも、下から来るか左から来るかの2パターンしかありません。下から来るのは先ほど数えたように2通り、左から来るのは1通り（スタートして上に2回行く場合のみ）だから、合計で3通りだとわかります。

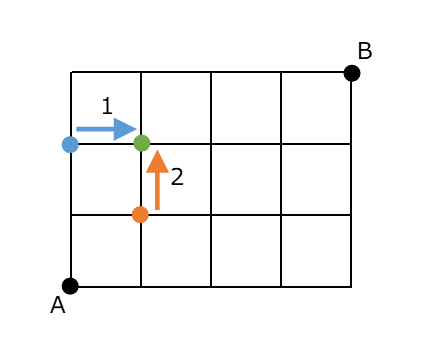
こうしていくと、すべての点について、順番に計算していくことができます。どの点も、左から来るか下から来るかの2パターンしかなく、左の分岐点への最短経路の総数が $L$ 通り（分岐点がない場合は0通り）で、下の分岐点への最短経路の総数が $D$ 通り（分岐点がない場合は0通り）なら、その点への最短経路の総数は $(L+D)$ 通りとなります。

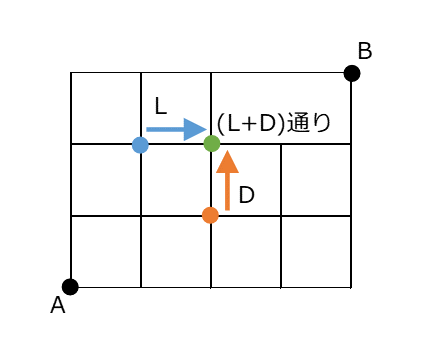
この考えをもとにしてコードをかいてみましょう。点A から右に $m$ 移動し、上に $n$ 移動した点への最短経路の総数を dp[m][n] で求められるようにします。

#include <iostream>
#include <vector>
using namespace std;

int main() {
  int m, n;
  cin >> m >> n;
  vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));

  for(int i = 0; i <= m; i++) {
    for(int j = 0; j <= n; j++) {
      if (i == 0 && j == 0) {
        dp[0][0] = 1;
      } else {
        int l = (i > 0)? dp[i - 1][j]: 0;
        int d = (j > 0)? dp[i][j - 1]: 0;
        dp[i][j] = l + d;
      }
    }
  }
  cout << dp[m][n];
  return 0;
}

dp[i][j] は、点A から右に $i$ 移動し、上に $j$ 移動した点への最短経路の総数を表しています。左から来る場合と下から来る場合（ない場合は0とする）を考え、これを足したものがその点への最短経路の総数となります。なお、一番はじめの dp[0][0] は、「何も動かない」という経路が1つあると考えています。こうすることで、dp[1][0] や dp[0][1] にうまく経路の数が入り、他の点への最短経路の総数もうまく計算できるようになります。

この考え方は、点 $(m,n)$ への最短経路の総数を、点 $(m-1,n)$ への経路と 点 $(m,n-1)$ への経路に分けて考えており、動的計画法を使って組合せの総数を計算していることになります（参考：フィボナッチ数列と再帰関数（メモ化再帰））。

また、メモ化再帰で書くなら、次のようになります。

#include <iostream>
#include <vector>
using namespace std;

vector<vector<int>> memo;

int dp(int x, int y) {
  if (x < 0 || y < 0) return 0;
  if (memo[x][y] != -1) return memo[x][y];

  if (x == 0 && y == 0) memo[x][y] = 1;
  else memo[x][y] = dp(x - 1, y) + dp(x, y - 1);

  return memo[x][y];
}

int main() {
  int m, n;
  cin >> m >> n;
  memo.resize(m + 1, vector<int> (n + 1, -1));

  cout << dp(m, n);
  return 0;
}

ゴールからさかのぼって計算しています。まずはメモ用の配列に -1 を格納し、計算結果が判明したらこの配列を更新していくようにしています。更新の仕方は、今まで通り、左から来るか下から来るかを場合分けして足しています。

２つの計算方法の比較

点 $(0,0)$ から 点 $(m,n)$ に移動する方法の総数を、2つの方法で計算しました。1つ目は、 $m+n$ 回の移動のうち、右に移動する $m$ 回をどう選ぶか、と考えて ${}_{m+n} \mathrm{C}_m$ 通り、と求める方法でした。この計算は、 $\dfrac{(m+n)!}{m!n!}$ を計算することで求められます。

一方、2つ目の方法は、各点について、左から来るか下から来るかの2通りしかないので、dp[i][j] = dp[i - 1][j] + dp[i][j - 1] を繰り返し計算することで求める方法でした。

考え方も式も違いますが、両者は同じものを計算しています。この2つの式の関係は、別の機会にもう少し見ることにしますが、計算方法に関する性質をここでは見ておきます。

$m,n$ が大きくなると、経路の総数はすごく大きな値になります。そのため、競プロでは、「1000000007 で割った余りを求めなさい」と出題されることが多いです。

1つ目の計算方法では、 $(m+n)!$, $m!$, $n!$ を $10^9+7$ で割った余りの計算はできるのですが、 $(m+n)! \div m!n!$ の商を $10^9+7$ で割ると余りがどうなるかは、簡単には計算できません。余りの計算では、商の余りに関する計算がありませんが、実はこの計算は少し難易度が高いのです。

一方、2つ目の計算では簡単です。dp[i][j] = dp[i - 1][j] + dp[i][j - 1] を計算するときに、右辺を $10^9+7$ で割って余りを計算すればいいです。和の場合であれば、余りはすぐに出せます。

競プロでは、 $m+n$ が10000程度であれば、2つ目の方法を使って計算しても間に合うため、2つ目の方法がよく使われます。

おわりに

ここでは、2方向だけに進める場合の最短経路の総数を求める問題を見ました。組合せで計算する方法と、動的計画法を使って計算する方法を見ました。余りを計算しないといけない場合には、今の時点では後者の方法しかできませんが、将来的には、前者で解く方法も見ることになります。

なお、数学の内容として学びたい場合は、【標準】最短経路の数 や 【応用】最短経路の数 が参考となるでしょう。