🕒 2019/10/04 🔄 2024/10/16

整数の掛け算

🏇

ここでは、整数の掛け算について見ていきます。コードは、C++を前提として書いています。 $(-4)\times(-3)=12$ などの計算がわかるなら、このページは読み飛ばしてもいいでしょう。

📘 目次

正の整数を掛ける

$0$ に、同じ正の整数を何回か足してみます。

#include <iostream>
using namespace std;

int main() {
  int ans = 0, a = 4, b = 3;
  for (int i = 0; i < b; i++) ans += a;
  cout << ans; // 12
  return 0;
}

上の計算では、 $4$ を $3$ 回足したため、 $4+4+4=12$ を足したことになります。このように、同じものを何度も足す計算を、「 $a$ に $b$ を掛ける」「 $a$ と $b$ を掛ける」「 $a$ を $b$ 倍する」などといいます。この計算を掛け算(かけざん、multiplication) といいます。

数学の世界では、掛け算を $a\times b$ や $a\cdot b$ と表します。また、文字を用いた式では、掛け算の記号を省略して、 $ab$ とも表します。逆にいうと、計算記号がない場合は掛け算を表している、掛け算記号が省略されている、ということです。

正の整数と正の整数とを掛ける場合、次のような図に対応させて考えることができます。

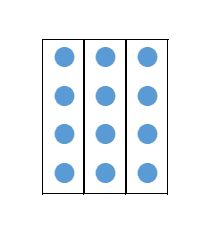
上の図は、縦に4つの丸を並べたものを1セットとして、横に3セット並べたものです。このときの丸の数は、4を3回足したものなので、 $4\times 3$ に対応します。

この図の縦と横に名前を付けてみます。横向きには文字を、縦向きには数字を対応させます。

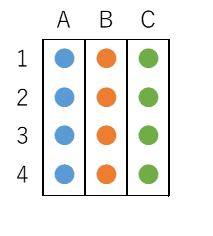
これを利用すれば、A1やB3のようにして、場所を特定することができます。文字と数字で場所を特定するには、次のような組み合わせが考えられます。

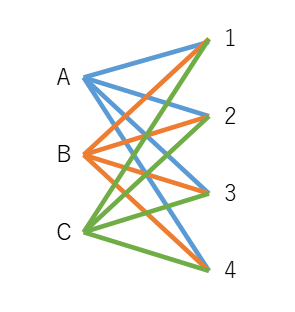
こうすると、掛け算が掛け合わせに対応しているように感じられるんじゃないかと思います。

コードでは、掛け算をa * bで表します。アスタリスクという記号を使っています。コードでは、掛け算の記号を省略することはできません。先ほどの計算は次のように書きます。

#include <iostream>
using namespace std;

int main() {
  int a = 4, b = 3;
  cout << a * b; // 12
  return 0;
}

掛け算は、乗算や乗法ともいいます。掛け算の答えのことを、積(product) といいます。先ほどの計算は、「 $4$ と $3$ の積は $12$ だ」ということができます。

負の整数に正の整数を掛ける場合も、同じように考えます。 $-4\times 3$ は $-4$ を $3$ 回足すことなので、 $-12$ となります。負の整数に正の整数を掛けるときは、符号を考えずに計算して、最後にマイナスをつければ計算できます。

ここでは説明のために足し算を使いましたが、掛け算を足し算で書くことは普通はありません。 $N$ を掛ける場合、足し算を使うと計算回数が $N$ 回になってしまいますが、掛け算を使えば1回の計算で済むからです。

掛け算を使えば、AtCoder ABC 080 A - Parkingなどの問題が解けるようになります。

$a$ に $2$ を掛けることは、2倍するといいますが、単純に「倍」と言ったりします。「給料が倍になった」といったら、2倍になったということです。本当になるといいんですけどね。

これを踏まえると、AtCoder ABC 004 A - 流行ができるでしょう。

負の整数を掛ける

先ほどは $a=4$, $b=3$ のときに、 $a\times b$ を考えましたが、 $a=4$, $b=-3$ ならどうなるかを考えてみます。

$-3$ 回足す、というのは考えづらいので、負の整数の足し算や引き算のときと同じように、回数を減らしていくとどうなるかを考えてみます。

足す回数を、3回、2回、1回と減らしていくと、結果は $4$ ずつ減っていきます。0回では0になります。さらに3回減らせば、 $4\times 3=12$ だけ減ることがわかります。並べて書いて見ると、次のようになります。
\begin{array}{ccccc}
4 & \times & 3 &=& 12 \\
4 & \times & 2 &=& 8 \\
4 & \times & 1 &=& 4 \\
4 & \times & 0 &=& 0 \\
4 & \times & (-1) &=& -4 \\
4 & \times & (-2) &=& -8 \\
4 & \times & (-3) &=& -12 \\
\end{array}結論としては、正の整数に負の整数を掛ける場合は、符号を考えずに掛け算をして、最後にマイナスをつければOKということです。

なお、細かいですが、数学の世界では、計算に使う記号を連続して書くことはありません。そのため、 $4\times -3$ とは書かずに、カッコでくくって $4\times (-3)$ と書きます。

負の整数に負の整数を掛ける場合も同じように考えてみましょう。 $-4\times(-3)$ を考えてみます。足す回数を3回、2回、1回と減らしながら結果を書いていくと、次のようになります。
\begin{array}{ccccc}
-4 & \times & 3 &=& -12 \\
-4 & \times & 2 &=& -8 \\
-4 & \times & 1 &=& -4 \\
-4 & \times & 0 &=& 0 \\
-4 & \times & (-1) &=& 4 \\
-4 & \times & (-2) &=& 8 \\
-4 & \times & (-3) &=& 12 \\
\end{array}結論としては、負の整数に負の整数を掛ける場合は、符号を考えずに掛け算をすればいいということです。負の整数と負の整数との積は、正の整数となります。

これらのことを実際にコードをかいて確かめてみましょう。

#include <iostream>
using namespace std;

int main() {
  int a = 4, b = -3, c = -4;
  cout << a * b << "\\n"; // -12
  cout << c * b << "\\n"; // 12
  return 0;
}

上で見た内容と同じ結果になっていますね。

また、ここまでに見た内容からもわかる通り、何かの数に $0$ を掛けると、積は $0$ になります。 $0$ を掛けることは $0$ 回足すということなので、何も足さない＝ $0$ ということです。また、 $0$ に何かの数を掛けても、積は $0$ になります。 $0$ を何回足しても $0$ だからです。

ここまでの内容を踏まえると、AtCoder ABC 098 A - Add Sub Mulなどができるようになります。手計算した答えとあわせることができるでしょう。

おわりに

ここでは、整数の掛け算について見てきました。掛け算は、足し算をまとめて計算する処理です。

負の数に負の数を掛けると正の数になるのは不思議かもしれませんが、「負の数を引くこと」が「正の数を足すこと」と同じであることに関連付けて考えれば、不思議さは減るかもしれません。もしくは、数学の内容として、【基本】正負の数の乗法（移動で考える）を見てみましょう。向きを考慮して考えると、マイナス掛けるマイナスがプラスになることがわかりやすくなるかもしれません。