🕒 2019/10/14 🔄 2024/10/16

倍数と約数

🦁

ここでは、倍数と約数について見ていきます。競プロでは、整数の性質に関連する問題も多く出題されます。倍数と約数は、整数の基本的な事項なので、以下で見ていきましょう。なお、コードはC++で書いています。

📘 目次

倍数

2つの整数 $a, b$ について、 $a$ が $b$ で割り切れるとき、 $a$ は $b$ の倍数(multiple) といいます。例えば、 $12$ は $4$ の倍数です。

$a$ が $b$ の倍数であるかどうかは、 $a$ が $b$ で割り切れるかどうかを確認すればよく、そのためには、余りが0になるかどうかを確認すればいいです。そのため、C++では、次のように書きます。倍数なら Yes 、違うなら No と返ってきます。

#include <iostream>
using namespace std;

int main() {
  int a = 12, b = 4;
  string ans = (a % b == 0)? "Yes" : "No";
  cout << ans;
  return 0;
}

整数 $a$ を1倍したもの、2倍したもの、3倍したもの、… はすべて $a$ の倍数なので、倍数は無限個存在します。100までの倍数を順番に書き出すコードは次のようになります。

#include <iostream>
using namespace std;

int main() {
  int a = 4, i = 1;
  while (a * i <= 100) {
    cout << a * i << "\\n";
    i++;
  }
  return 0;
}

$a$ が $b$ の倍数であるとき、 $a$ を $b$ で割ったときの余りが $0$ なので、ある整数 $q$ を用いて、 $a=bq$ と書けます。この $q$ は0や負の数でもかまいません。そのため、例えば、 $0$ や $-8$ なども $4$ の倍数です、一般に、倍数は負の整数を含めた範囲で考えます。特に正の値に制限したい場合は、「正の倍数」と明記されていることが普通です（例：AtCoder ABC 106 B - 105）。

偶数と奇数

倍数の中でも、特に2の倍数は偶数(even) といいます。整数のうち、偶数ではないものを奇数(odd) といいます。つまり、偶数とは、2で割った余りが0の整数のことで、奇数とは2で割った余りが1の整数のことです。

このことから、整数 $a$ が偶数か奇数かを判定するには、2で割った余りを考えればいいです。次のコードは、偶数なら Yes と出力し、奇数なら No と返します。

#include <iostream>
using namespace std;

int main() {
  int a = 9;
  string ans = (a % 2 == 0)? "Yes" : "No";
  cout << ans;
  return 0;
}

これを踏まえれば、AtCoder ABC 086 A - Productなどができるようになります。

約数

2つの整数 $a, b$ について、 $a$ が $b$ で割り切れるとき、 $b$ は $a$ の約数、といいます。倍数のときと主語が違っている点に注意しましょう。記号では、 $b\mid a$ と書きます。例えば、 $4$ は $12$ の約数です。特に、どんな整数 $a$ に対しても、 $1$ は必ず $a$ の約数になります。

$b$ が $a$ の約数であることは、 $a$ が $b$ で割り切れるかどうかを確認すればいいので、倍数のときと同じコードで確認することができます。$a$ の約数も、正と負の両方が考えられるので、正の値に限定したい場合は、「正の約数」といいます。

正の整数 $a$ と $a$ の約数を比べたとき、約数のほうが大きくなることはありません。そのため、約数は有限個しかありません。有限個しかないので、すべてを列挙することができます。次のコードは、正の約数を列挙するC++のコードの例です。

#include <iostream>
using namespace std;

int main() {
  int a = 12;
  for (int i = 1; i <= a; i++) {
    if (a % i == 0) cout << i << "\\n";
  }
  return 0;
}

これを踏まえれば、AOJ ITP1_3_D How Many Divisors?ができるようになるでしょう。

約数の列挙再考

先ほど、約数を列挙するコードを見ました。これを実行すると、1, 2, 3, 4, 6, 12 という数字が並びます。もちろん、たしかにどれも12の約数になっています。約数かどうかを小さい順からチェックしているので、結果も小さい方から順番にすべて列挙されます。

ここで、最初と最後を掛けると、どうなるでしょうか。また、前から2番目と後ろから2番目、前から3番目と後ろから3番目と掛けてみるとどうでしょう。どれも12になりますね。逆に考えると、後半の3つは、前半の3つで12を割ればすぐに求められていた、ということです。

実は、約数の個数を数えるのに、12個全部をチェックする必要はありません。例えば、 $3$ が約数だとわかれば、 $12\div 3=4$ なので $4$ も約数だとすぐにわかります。それは、次の図を考えればわかるでしょう。

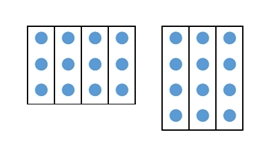
$12\div 3$ が割り切れることを図にすると、上の左側のようになります。縦に3個並べたものを1セットにして区切っていくと、4列できて余りはありません。この縦と横を入れ替えれば、右側のように、縦に4個並べたものを1セットにして、3列できます。このように、縦が横より長いものは、縦のほうが短いケースを回転させればいいわけです。

特別なケースとして、縦と横が同じになるケースもあります。例えば、 $a=4$ のときは、縦に2個並べると列は横に2つできます。この場合は、縦に並べた $2$ が約数だとわかります。

結局、考えるべきなのは、縦が横以下のケースだけでいいということです。ここまでの内容を踏まえると、約数を列挙するコードは次のように書き換えられます。正の整数を入力すれば、その約数をすべて列挙します。ただ、小さい順にはなりません。

#include <iostream>
using namespace std;

int main() {
  int a; cin >> a;

  for (int i = 1; i * i <= a; i++) {
    if (a % i == 0) {
      int j = a / i;
      if (i == j) {
        cout << i << "\\n";
      } else {
        cout << i << "\\n";
        cout << j << "\\n";
      }
    }
  }
  return 0;
}

先ほどのように、 $a$ 個の丸を並べることを考えると、上のコードは、縦に $i$ 個並べて余りなく並べられるかを調べていることに対応しています。縦が横以下のケースだけを考えればいいので、i * i <= a としています。i * i が a を超えれば、縦が横以下になることはありません。次の図は、 $a=15$, $i=4$ のときの例ですが、これを参考に考えてみるとわかると思います。

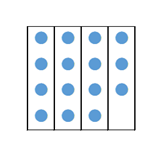
i * i が a を超えて以降は、縦を伸ばすと横は短くなる一方なので、「縦が横以下」のケースは今後現れません。

こうして、上のコードでは i * i <= a の範囲で、縦に $i$ 個並べたときに、横に $j$ 列できて余りが出ない場合を考えるようにしています。縦と横が同じ長さなら縦の長さだけを出し、違うなら縦と横の長さを出力します。こうして、ダブることなく、正の約数がすべて列挙されます。

これで計算する回数はどれくらい減るでしょうか。例えば、 $a=12$ の場合は、for文を3周すればおしまいです。 $a=100$ なら、 $i=10$ のときが最終なので10周です。 $a$ が1億なら、 $i$ が1万のときが最終なので1万周です。このことからわかる通り、 $a$ の数が大きくなるほど、for文の中を繰り返す回数は大幅に減ることがわかります。

おわりに

ここでは、倍数と約数について見てきました。整数に関する競プロの問題の中ではもっとも基本的な事項です。

数学の内容として学びたい場合は、【基本】約数と倍数が役立つでしょう。