数の大小
ここでは、数の大小や、それにまつわる話題を見ていきます。数直線や絶対値を紹介します。
数直線
数を扱うときに、図を使った方がわかりやすくなることがあります。次のような図がよく使われます。

これは、数直線(number line) といいます。左右に伸びた直線に、基準となる点(原点)をとり、そこに $0$ を対応させます。また、 $0$ より右側に点をとって、 $1$ を対応させます。 $1$ の次の数をその右へ、その次の数をその右へ、と他の数字も対応させていきます。 $0$ の左側には負の数を対応させます。
$0$ と $1$ までの長さを10等分すれば、 $0.1$, $0.2$ といった数も対応させることができます。さらに分割を多くすれば、各点と数(整数と小数を含めたもの)とを対応させることができます。
つまり、数直線とは、直線上の点と数とを、一対一に対応付けしたもの、ということです。数直線上の点に対応している数字のことを、その点の座標(coordinate) といいます。
競プロの問題でも、数直線の上を動くような問題が出ることがあります(例:AtCoder ABC 117 C - Streamline)。直線上の点と数とが対応していることがわかっていれば、問題文の意味はわかるでしょう。
絶対値
後で見るように、数直線では、原点からどれだけ離れているかが、1つの重要な情報となります。そのため、これには特別な名前がついています。数直線上で、原点から対応する点まで距離のことを、その数の絶対値(absolute value) といいます。絶対値は0か正の値をとり、負の値になることはありません。
数学では、 $|$ という記号2つで、数字をはさんで使います。例えば、 $2$ も $-2$ も、原点から $2$ だけ離れているので、 $|2|=2$, $|-2|=2$ となります。
コードでは、言語によって絶対値の表し方は異なります。C++の場合は、abs という関数を用います。
#include <iostream>
using namespace std;
int main() {
int a = 2, b = -2;
cout << abs(2) << "\\n"; // 2
cout << abs(-2) << "\\n"; // 2
return 0;
}言い換えると、 $|a|$ は、 $a$ が $0$ か正の数なら $a$ と等しく、 $a$ が負なら $-a$ と等しい、ということです(負の数にマイナスをつけたものは、別の機会に扱います)。
数の大小
2つの数 $a,b$ を数直線で考えた際、右にある方を「大きい」といい、左にある方は「小さい」といいます。 $2$ と $4$ なら、 $4$ のほうが右にあるので、「 $4$ は $2$ より大きい」となります。

$0$ からインクリメントし続けたとき、後に出てくるほど大きいということです。
符号が異なる場合、例えば、 $a$ が正で $b$ が負とします。数直線で考えると、 $a$ は原点の右、 $b$ は原点の左なので、 $a$ のほうが大きいことがわかります。
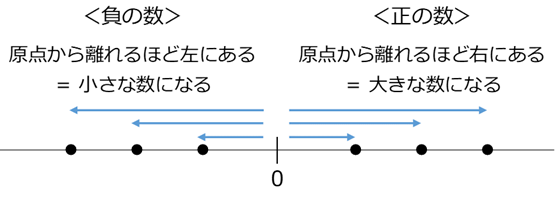
$a,b$ がともに正のときは、原点から離れるほど、右に行くので、絶対値が大きいほど大きくなります。
$a,b$ がともに負のときは、原点から離れるほど、左に行くので、絶対値が大きいほど値は小さくなることがわかります。 $-2$ と $-4$ なら、 $-4$ のほうが左にあるので、「 $-4$ は $-2$ より小さい」となります。

$0$ からデクリメントし続けたとき、後に出てくるほど小さいということです。
絶対値が大きいときに値が大きいのか小さいのかは、正の数か負の数かによって変わってくるので注意しましょう。
不等号
数の大小関係を表すものを、不等号といいます。記号は4種類あり、それぞれ次のような意味を持っています。
| 記号 | 意味 |
|---|---|
| $a\\gt b$ | $a$ が $b$ より大きい |
| $a\\lt b$ | $a$ が $b$ より小さい( $a$ は $b$ 未満) |
| $a\\geqq b$ | $a$ が $b$ と等しいか $b$ より大きい( $a$ は $b$ 以上) |
| $a\\leqq b$ | $a$ が $b$ と等しいか $b$ より小さい( $a$ は $b$ 以下) |
口が広がっている方が大きいことを表しています。
高校までの数学の教科書では、 $\geqq$, $\leqq$ の記号を使いますが、サイトや本によっては $\geq$, $\leq$ を用いることもあります(AtCoderではどちらのスタイルも使われています)。2本線でも1本線でも、意味は同じです。
$a\geqq b$ は、 $a$ と $b$ が等しくても構いません。例えば、 $5\geqq 5$ は正しい式です。また、「5以下」「5以上」といったら、5も含みます。「5未満」といったら、5は含みません。競プロでは、境い目が重要になることがあるので、境界部分は正しく把握しましょう。
コードでは、 $\gt$, $\lt$ の記号はそのまま用いますが、 $\geqq$, $\leqq$ はそのままは使いません。多くの言語では、それぞれ、>=, <=と書きます。
先ほど見た内容をもとに、数の大小を比較した結果をいくつか書いておきましょう。
#include <iostream>
using namespace std;
int main() {
int a = 4, b = 2, c = 0, d = -1, e = -3;
cout << (a > b) << "\\n"; // 1
cout << (c >= b) << "\\n"; // 0
cout << (d < e) << "\\n"; // 0
cout << (d <= b) << "\\n"; // 1
return 0;
}結果が1なら不等式が成り立つことを表し、0なら成り立たないことを表しています。不等号と、ifやandの使い方がわかっていれば、AtCoder ABC 061 A - Between Two Integersなどができるでしょう。
2つの整数 $a,b$ があったとき、数直線では、
- $a$ が $b$ より右にある
- 2つが同じ位置にある
- $a$ が $b$ より左にある
の3つしかありません。また、このうちのどれか1つだけが成り立ちます。なので、 $a\gt b$, $a=b$, $a\lt b$ のどれか1つだけが成り立ちます。また、 $a\geqq b$, $a\lt b$ のどちらか片方が必ず成り立つ、などともいえます。(これらの結果は、整数に限らず、小数でも成り立ちます)
こうした内容を踏まえると、AtCoder ABC 053 A - ABC/ARCなどができるようになります。
$a,b$ の大小を比べているときに、 $a$ のほうが大きいときに、「同じではない」ことを強調したい場合、「真に大きい」と言ったりします。例えば、AtCoder ABC 083 C - Multiple Giftの問題文中に出てきています。
大きい方と小さい方
競プロでは、2つの数を比較して、大きい方を選ぶとか小さい方を選ぶ場面が多く出てきます。毎回 if と不等号を使ってもいいのですが、多くの言語では、max と min が用意されています。
#include <iostream>
using namespace std;
int main() {
int a = 13, b = 8;
cout << max(a, b) << "\\n"; // 13
cout << min(a, b) << "\\n"; // 8
cout << min(a, a) << "\\n"; // 13
return 0;
}13と8を比較しています。1つ目は大きい方、2つ目は小さい方が返っていることがわかります。最後は、13と13を比較しています。この場合は、13が返ってきます。同じ値のときは、その値が返ってくるということです。同じ値のときは、「小さい方」というのは存在しないので、厳密に書きたい場合は「大きくない方」ということもあります。
これを踏まえると、AtCoder ABC 002 A - 正直者ができるようになります。
おわりに
ここでは、数の大小に関連するトピックを見てきました。図を使いたい場合は、数直線を使うといいと思います。
数学として学びたい人は、中学生向けですが、以下の記事が参考になるでしょう。