整数の四則演算

ここでは、整数の四則演算について、いくつかの重要な性質を見ていきます。

四則演算

整数同士の計算として、足し算、引き算、掛け算、割り算について見てきました。これら4つの計算をまとめて、四則演算といいます。計算の中でも最も基本的なものです。

これらの計算をコードでどのように書くかがわかっていれば、AOJ ITP1_4_C Simple Calculatorができるでしょう。

足し算の順番

正の整数 $a,b$ に対して、 $a+b$ とは、 $a$ に $b$ 回インクリメントを行うことでした（参考：整数の足し算と引き算）。これは、次のような図で考えることもできます。

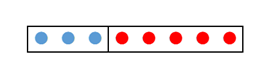
まず、左側に3個の青丸を置きます。次に、1つずつ、合計5個の赤丸を置きます。上の図は、すべての丸を置き終わった後の図です。この丸の数は、 $3+5$ となります。

ただ、これは、右から置いた、とみることもできます。つまり、右側に赤丸5つを置いて、その後に、左側に3個の青丸を1つずつ置いていった図とも考えられます。そう考えるなら、上の丸の数は、 $5+3$ と書けるでしょう。

左から数えるか右から数えるかで答えが変わるはずはないので、 $3+5=5+3$ となることがわかります。これは一般的に成り立ちます。つまり、 $a+b=b+a$ はつねに成り立ちます。足す順番を変えても計算結果は変わりません。

掛け算の順番

正の整数 $a,b$ に対して、 $a\times b$ とは、 $a$ を $b$ 回足すことを表しているのでした（参考：整数の掛け算）。これは、次のような図で考えることもできます。

まず、左側の1列に、3個の青丸を置きます。次に、右へ右へと列を増やし、5列になるまで同じように丸を置いていきます。この丸の数は、 $3\times 5$ となります。

では、この図の線の入れ方を変えてみます。

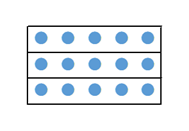
今度は、はじめに上の段に5個の丸を置き、同じものを合計3段作ったと考えます。こう考えるなら、丸の数は $5\times 3$ と書けます。

完成図が同じなのに置き方を変えただけで丸の数が変わるはずはないので、 $3\times 5=5\times 3$ となります。これは一般的に成り立ちます。つまり、 $a\times b=b\times a$ が成り立ちます。掛ける順番を変えても計算結果は変わりません。

学校で習った計算方法を覚えている人にとっては当たり前すぎて、何の役に立つのかわかりにくいと思いますが、競プロでは、約数や素数を考えるときなどで、計算回数を減らすために利用することができます。

四則の混じった計算

ここまでは、 $a+b$ など、2つの数の計算を考えてきましたが、もっとたくさんの数を含んだ計算も考えることができます。そのときには、計算をする順番にルールがあります。

基本的には、左から計算します。 $1+2+3+4$ は、左から順番に計算して $10$ と求めます。

ただし、掛け算と割り算は、足し算と引き算よりも優先的に計算することになっています。 $5-4\times 3$ は、左の引き算ではなく、右の掛け算から計算し、 $5-12$ としてから $-7$ と計算します。

もし、足し算や引き算を、掛け算や割り算よりも先に計算したい場合は、カッコでくくります。先ほどの計算で引き算のほうから先に計算したいなら、 $(5-4)\times 3$ とかきます。こうすれば、 $1\times 3=3$ という計算になります。

コードでも、これらの順番のルールは同じです。数学とコードで少し違うところは、カッコのかき方です。数学の場合は、カッコを複数使う場合は、カッコの種類を変えますが、コードではいつも丸カッコを使います。

足す順番や掛ける順番は変えても結果は変わりません。引く場合は、引き算の記号ごと入れ替えれば、結果は変わりません。例えば、 $10-9$ は、 $-9+10$ と結果が同じになります。

割り算は少しやっかいです。C++などでは、計算結果が切り捨てられてしまうので、順番を入れ替えると計算結果が変わってしまう可能性があります。次の計算式は、数学ではどちらも $15$ ですが、コード上は違ったものになります。

#include <iostream>
using namespace std;

int main(){
  int a = 5;
  cout << a * (a + 1) / 2 << "\\n"; // 15
  cout << a / 2 * (a + 1) << "\\n"; // 12
  return 0;
}

C++では 5 / 2 が切り捨てられて 2 と計算されてしまうために、違いが生じています。意図して計算しているなら問題ありませんが、前者のつもりで計算しているなら、切り捨ての可能性を考えて正しく書く必要があります。

総和

足し算の答えを和といいますが、たくさんある数字をすべて足したものを、総和ということがあります。競プロでは、「条件を満たすものの総和を求めなさい」といった形式で出題される問題があります。

例えば、AtCoder ABC 083 B - Some Sumsなどです。各桁の数字の出し方がわかっていれば、挑戦してみましょう。また、AtCoder ABC 037 C - 総和も、問題の内容は理解できるでしょう。実際に解くには、少しテクニックが必要です。

約分

掛け算と割り算が混じった、次のような式を見てみましょう。\[ (6\times 3)\div (2\times 3) \]これは次と同じ式です（参考：整数の割り算）。\[ \frac{6\times 3}{2\times 3} \]普通は、それぞれの掛け算を先にしてから、割り算を行います。しかし、これは $\dfrac{6}{2}$ と同じ結果になります。両方から $\times 3$ が消えています。なぜこの2つの計算が同じ答えになるかは、次の図を見るといいでしょう。

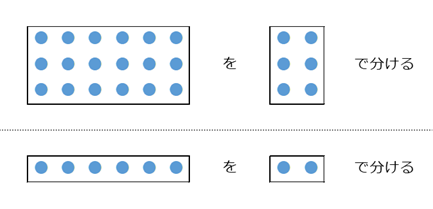
上側は、 $6\times 3$ 個の丸を $2\times 3$ 個入る箱に分けようとしています。 $2\times 3$ 個ずつに分けるということです。下側は、縦の長さを $1$ にしたものです。これを見てもわかる通り、縦が同じ長さなら、「何を何で分けるか」を考えた結果は変わらないことがわかるでしょう。

一般的に書くと、 $ac$ を $bc$ で割った結果は、 $c$ を掛ける前、つまり、 $a\div b$ と同じ結果になります。 $\dfrac{ac}{bc} = \dfrac{a}{b}$ が成り立つということです。右側のように変形すると、割り算に出てくる値が小さくなり、計算しやすくなります。

おわりに

では、整数の四則演算について見てきました。途中で出てきた図は単純なものですが、数学を学ぶ上でも競プロで問題を解く上でも役立つと思います。このサイトでも、説明するときに、何度か登場します。