フェルマーの小定理

ここでは、商の剰余演算で今後使うことになる、フェルマーの小定理とその証明を見ていくことにします。

フェルマーの小定理の内容

商と剰余演算の具体例でみたように、 $m \div a \pmod p$ を計算するには、 $a^x\equiv 1 \pmod p$ となるような $x$ が見つかればいいのでした。もし見つかれば、 $a^x$ を掛けることで、答えに影響を与えることなく、割り算を掛け算に変形することができるのでしたね。

一般に、このような $x$ をやみくもに探して見つけるのは大変で、あるかどうかもわかりません。しかし、ある条件を満たせば、次のようにして簡単に見つけられることが保証されています。

このことを、フェルマーの小定理といいます。

例えば、 $p=7$ の場合を考えてみましょう。 $1$ から $6$ までの整数は、どれも $7$ と互いに素なので、この定理が使えます。つまり、この定理は、 $1^6$, $2^6$, $3^6$, $4^6$, $5^6$, $6^6$ は、どれも $7$ で割った余りが $1$ になる、と主張しているわけです。これくらいの数であれば実際に計算して確かめることができるので、気になる人はやってみましょう。

以下では、フェルマーの小定理の証明を見ていきます。なお、証明方法はいくつかあり、以下で紹介する方法以外にもあります。

具体的な場合でフェルマーの小定理の証明を考える

さて、フェルマーの小定理の証明を行いますが、一般的な場合をいきなり考えるのは少し難しいので、まずは具体的な値を使って様子を見ましょう。 $p=7$ の場合を考えることにします。

次の図のように、 $0$ から $6$ までの整数を時計回りに書いていきます。これは余りを表すつもりでかいています。

このとき、 $0$ から出発して、1個時計回りに移動して線を結ぶ、というのを、繰り返してみます。できあがる図は、次のような七角形になります。

次に、 $0$ から出発して2個ずつ移動して線を結ぶように変えてみます。今度は、次のような図形になります。

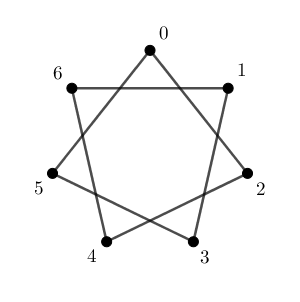
これは、 $0$ から出発して、 $2,4,6,8,10,12,14$ 個移動した点を順番に結んでいってるわけですね。例えば5回移動した後、つまり、10個移動した後では、3の点にいます。これは、10を7で割った余りが3であることに対応しています。

上の図を見ると、再び $0$ に戻ってくるまでに、すべての点を1回ずつ通っていることがわかります。このことはあとで使います。

続いて、3個ずつ移動した場合も考えてみます。

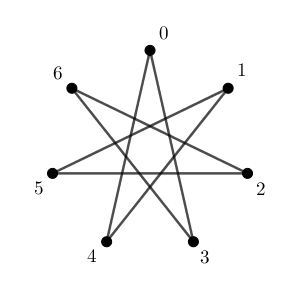
今度は、 $0$ から出発して $3,6,9,12,15,18,21$ 個移動した点を順番に線で結んでいってます。この場合も、 $0$ に戻ってくるまでにすべての点を1回ずつ通ってます。

同様に、4個ずつ、5個ずつ、6個ずつ移動する場合も考えてみましょう。実際にやってみるとわかりますが、上の3つのケースと同じになります。4個ずつ移動した場合は、3個ずつ移動した場合と同じで、5個ずつと2個ずつ、6個ずつと1個ずつも同じ図になります。

さて、 $0$ を出発してから、7回移動すると再び $0$ に戻ってきます。移動した回数が $7$ の倍数になるから、不思議ではありません。もう一つ上の図でわかることは、この間、同じ場所は通らない、ということです。これは少し不思議に思うかもしれませんが、よく考えるとこれも当たり前です。

もし $a$ 個ずつ移動したときに（ $a$ は $1\leqq a \leqq 6$ を満たす整数）、 $i$, $j$ 回目で $(1\leqq i \lt j \leqq 6)$ 同じ場所にいるとすると、 $a(j-i)$ が7の倍数にならないといけません。が、 $a$ も $j-i$ も 1以上6以下の値であり、 $7$ が素数なのでそのようなことは起こりません。

このことから、 $a$ 個ずつ移動するなら、 $a$, $2a$, …, $6a$ を $7$ で割った余りは、すべて違う数であることがわかります。また、これらを $7$ で割って割り切れることはないので、余りに着目すると $1$ から $6$ までの数字が一回ずつ出てきます。上の図でいうと、 $0$ に戻るまでにすべての点を通ることに対応しています。

なので、次のような計算ができます。 $\bmod 7$ で計算しています。
\begin{eqnarray}
& &
a\cdot 2a\cdots 6a \\[5pt]
&\equiv&
(a \bmod 7)\cdot (2a \bmod 7) \cdots (6a \bmod 7) \\[5pt]
&\equiv&
1\cdot 2\cdots 6 \\[5pt]
\end{eqnarray}2行目から3行目は、 $a$, $2a$, …, $6a$ を $7$ で割った余りに、 $1$ から $6$ までの数字が一回ずつ出てくることを利用しています。

1行目の式は、 $a^6 6!$ と書け、最後の式は $6!$ と書けます（ $6!$ は6の階乗です。参考：和や階乗と再帰関数）。両辺の余りが同じなので、両辺の差は $7$ で割れます。つまり、 $6!(a^n - 1)$ が $7$ で割り切れるということです。ただ、 $1$ から $6$ の整数は $7$ と互いに素なので、結局、 $a^6-1$ が $7$ の倍数、つまり、\[ a^6\equiv 1 \pmod 7 \]となります。これがフェルマーの小定理の主張であり、これで $p=7$ のときにフェルマーの小定理が証明できたことになります。

一般の場合でフェルマーの小定理を考える

先ほどと同じ考え方で、一般の場合にも示すことができます。

$p$ は素数で、 $a$ は $p$ と互いに素な整数とします。

このとき、 $a,2a,3a,\cdots (p-1)a$ の中に、 $p$ で割ったときの余りが同じものはありません。これらの中から2つ抜きだして $ia$, $ja$ を考えたとき、 $i\ne j$ の場合は、 $(i-j)a$ が $p$ で割り切れることはないからです。

そのため、この $p-1$ 個の数を、それぞれ $p$ で割ると、余りは $1$ から $p-1$ までが1回ずつ出てきます。このことから、この $p-1$ 個の数をすべて掛けて $p$ で割った余りを考えると、\[ (p-1)! a^{p-1} \equiv (p-1)! \pmod p \]となります。ここで、 $(p-1)!$ は $p$ で割れないので、 $a^{p-1}\equiv 1$ となります。こうして、一般の場合でフェルマーの小定理を示すことができました。

おわりに

ここでは、フェルマーの小定理について見てきました。この定理を使うと、商の剰余演算ができるようになります。競プロでは、 ${}_n\mathrm{C}_k$ を $10^9+7$ で割った余りを計算することがありますが、この計算ができるようになります。具体的な計算方法については、別ページで見ることにします。