ユークリッドの互除法

ここでは、最大公約数を求めるために使う、ユークリッドの互除法について見ていきます。約数を調べたり素因数分解を利用するよりも、かなり簡単に最大公約数を求めることができるようになります。

縦と横が同じ長さの箱で区切る

最大公約数を求めるには、素直にやるなら、それぞれの約数を調べていくことになります。例えば、 12 と 18 の最大公約数を調べるなら、12 の正の約数を考えます。正の約数 1, 2, 3, 4, 6, 12 のうち、 18 の約数になっているもので一番大きいものは 6 です。なので、最大公約数が 6 だとわかります。

数字が小さいときはこの方法でもいいですが、大きくなると困ります。約数を調べるのが大変ですからね。しかし、数字が大きくても最大公約数を早く見つける方法があります。それが以下で紹介するユークリッドの互除法です。

ユークリッドの互除法についてみる前に、まずは図を使って考え方を見ることにしましょう。次の図は、縦に15個、横に21個の丸を並べたものです。これを利用して、15と21の最大公約数について考えてみます。

これを、縦1個横1個の箱で区切っていくと、上のように余りなくちょうど区切ることができます。しかし、縦2個横2個の箱では、うまく区切ることができません。

これは、15 や 21 が 2 で割り切れないことからもわかります。次に、縦3個横3個の箱で区切ってみましょう。

余りなくちょうど区切ることができます。これは、15 も 21 も 3 で割り切れる、つまり、3が公約数になっていることを表しています。続いて、縦5個横5個の箱で区切ってみると、次のようになります。

今度は、縦は余らないですが、横が余ってしまいます。これは、15は5で割り切れるけど、21が5で割り切れないことに対応します。つまり、5は公約数ではない、ということです。

以上のことから、公約数を見つけることは、上のように並べた丸を縦と横が同じ長さの箱で区切ったときに、余りなく区切れるものを見つけることに対応します。最大公約数は、そのような箱のうち、一番大きい箱に対応します。

残りの部分に着目する

公約数は、縦と横が同じ長さの箱で、余りなく区切れるものを見つけることに対応していて、最大公約数はそのような箱で一番大きいものに対応しているのでした。
これを踏まえて、次のようなことを考えてみましょう。

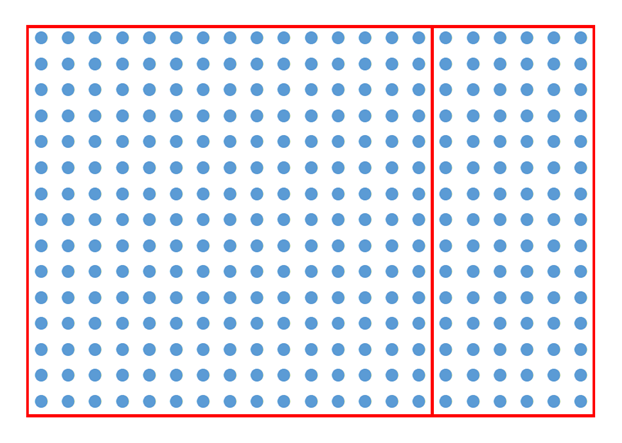
丸の部分を、2つの領域に分けています。左側は、縦と横が15個となっていて、右側は残りです。この2つの領域を、先ほどと同じように、「縦と横が同じ長さの箱」で区切っていくことを考えましょう。

もし、全体をうまく区切れたなら、左側だけの領域もうまく区切れているはずです。横は縦と同じ15個の丸があるからです。このことから、残りの右側の領域もうまく区切れていることがわかります。

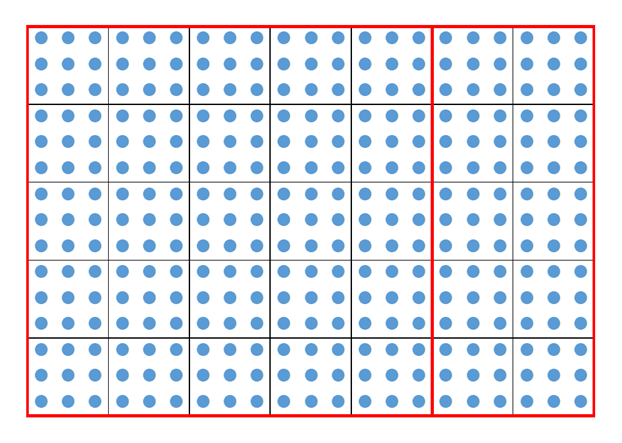
逆に、ある箱で右側の領域が余りなく区切れるなら、全体も余りなく区切れるはずです。縦の15を余りなく区切れるなら、左側の領域の横15も余りなく区切れるからです。

つまり、縦と横の長さが同じ箱で区切る場合、全体を余りなく区切ることと、右側を余りなく区切ることは、同じ結果になる、ということです。右側の部分のほうが小さいので、考えやすくなります。

結果として、（90度回転して）縦が6で横が15の丸を区切ることを考えればよくなります。

ここで、先ほどの技をもう一度使います。次のように分解して考えてみましょう。

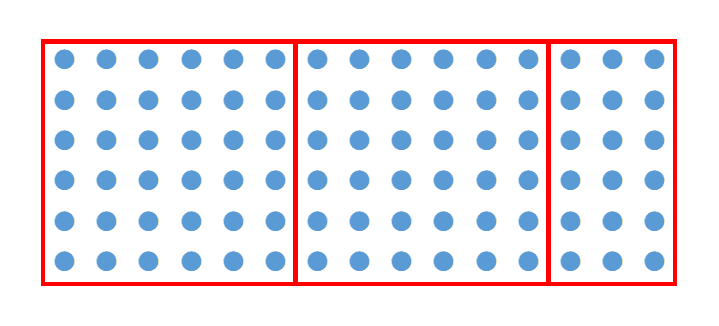
縦が6横が6の領域で区切ります。左側に2つできて、右側に残りが発生します。先ほどと同じように考えれば、全体を区切ることと、一番右側の部分を区切ることは、同じ結果になります。

こうして、（90度回転して）縦が3個で横が6個の丸を区切ることを考えればよくなります。

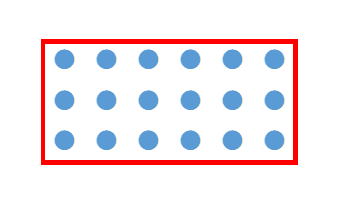
これは、次のようにして、縦3個横3個で区切るのが最大になることがわかります。

以上の結果から、「縦3個横6個」を区切るのも「縦6個横15個」を区切るのも「縦15個横21個」を区切るのも、余りなく区切れるのは「縦3個横3個の箱」が最大であることがわかります。この箱の最大値が最大公約数に対応しているので、こうして、15と21の最大公約数が3であることがわかりました。

分割した後の領域がどうなっているかも簡単にわかります。「縦15個横21個」を分割すると、「縦15個横15個」と「縦15個横6個」となりました。分割後の新しい横は、 $21-15$ で求められます。「縦6個横15個」を分割すると、分割後の一番小さい領域は「縦6個横3個」ですが、この横は $15$ から $6$ を何度も引いて余ったものになります。これは、割り算の余りに対応しています（参考：整数の割り算）。つまり、どんどん割った余りを考えていけばいい、ということです。

ユークリッドの互除法

ユークリッドの互除法は、上でみた手順を使って最大公約数を求める手法です。文字を使って説明すると次のようになります。

2つの正の整数 a, b の最大公約数を考えるとします。先ほどの箱の例を用いると、縦が b 個で横が a 個の丸を並べたと考えます。領域を分けて残った部分を考えましたが、この残りの部分の横には a % b 個の丸が並んでいます。この値が 0 なら、a が b の倍数なのだから、最大公約数は b です。 0 でない場合は、先ほどの箱の例のように、残った部分の縦と横を入れ替えて、縦が b 個、横が a % b 個並んだ丸に対して、新しく同じことを考えていきます。領域を分けていくと、どんどん小さくなるのでいつかはこの操作は終わります。

この手順をコードで書いてみます。

#include <iostream>
using namespace std;

int main() {
  int a, b;
  cin >> a >> b;

  while (a % b != 0) {
    int a2 = a;
    a = b;
    b = a2 % b;
  }
  cout << b;
  return 0;
}

a % b を調べて、0 だったら b が最大公約数、そうでないときは、 a, b を b, a % b に置き換えて再び余りを調べる、という流れです。a = b; の行で a の値が変わってしまうため、更新前の a の値を別の変数に格納しています。先ほどの例である 21, 15 などを入れて、結果を確かめてみましょう。

ユークリッドの互除法を使うと、最大公約数を速く求めることができます。約数を調べていく方法よりも、かなり速いです。上の箱の例を見てもわかるとおり、考えている値がどんどん小さくなることからもわかるでしょう。また、例えば、 899, 677 の最大公約数を求めてみましょう。どちらがすぐに求められるか、実感できるはずです。

再帰関数や三項演算子がわかるなら、次のようにして、最大公約数を求める関数を書くことができます。

int gcd(int a, int b) { return (a % b)? gcd(b, a % b): b; }

正の整数 a, b を入力すれば、最大公約数が返ってきます。ものすごくスッキリしましたね。

最大公約数を求めるのに一番思いつきやすい方法は、約数を調べていく方法でしょう。公約数の中で一番大きいものを最大公約数とする、というのがまず思いつく方法です。一方、ここで見たユークリッドの互除法を使う方法は、なぜこれで求められるか、理屈を理解するのは難しいですが、実装自体はすごく短くシンプルになります。また、処理も速くなります。求めるものが同じでも、どのように求めるかによって、実装の難易度や複雑さ、計算回数の多さなどはかなり違ってきます。

また、最小公倍数は、最大公約数からすぐに求められます。素因数分解と最大公約数と最小公倍数の最後で見たように、 $a,b$ の最小公倍数は、 $a,b$ の最大公約数で $a,b$ の積 $ab$ を割れば求められます。先ほどの gcd 関数を使えば、次のように求められます。

int lcm(int a, int b) { return a / gcd(a, b) * b; }

オーバーフローが発生しないように、先に割っています。gcd(a, b) は a の約数なので、この割り算はつねに割り切れます。こうして、最大公約数も最小公倍数もシンプルに求められます。

おわりに

ここでは、ユークリッドの互除法を使って、最大公約数を求める方法を見てきました。割って余りを考える、というシンプルな方法で最大公約数が求められるのは不思議ですね。

ここでは数学的な証明を載せていませんでしたが、数学の内容として学びたい場合は、【基本】ユークリッドの互除法の使い方 や 【標準】ユークリッドの互除法の原理 などが参考になるでしょう。