整数の割り算

ここでは、整数の割り算について見ていきます。コードは、C++を前提に書いています。

正の整数を正の整数で割る

ある正の整数から、ある正の整数を何回か引いてみます。0以上の範囲で、引けなくなるまで引いてみて、何回引けるかを数えてみます。

#include <iostream>
using namespace std;

int main(){
  int a = 15, b = 3, q = 0;
  while (a >= b) {
    a -= b;
    q++;
  }
  cout << q; // 5
  return 0;
}

上の計算では、 $15$ から $3$ を繰り返し引いています。 $3$ 以上なら、まだ引ける、と考えています。計算すると、5回引けることがわかります。このように、引ける回数を求める計算を、「 $a$ を $b$ で割る」といいます。この計算を割り算(division) といいます。

数学の世界では、割り算を $a\div b$ や $\dfrac{a}{b}$ と表します。コードでは、割り算をa / bで表します。そのため、先ほどの計算は次のように書きます。

#include <iostream>
using namespace std;

int main(){
  int a = 15, b = 3;
  cout << a / b; // 5
  return 0;
}

割り算は、除算（じょざん）や除法といい、割り算の結果を商(quotient) といいます。

割り算は日常でも使います。15個のお菓子を3人で分ける場合、1個ずつ配っていくと、5周しておしまいです。これはまさに、 $15\div 3=5$ の計算に対応していますね。コードで書いたことと同じ動きです。

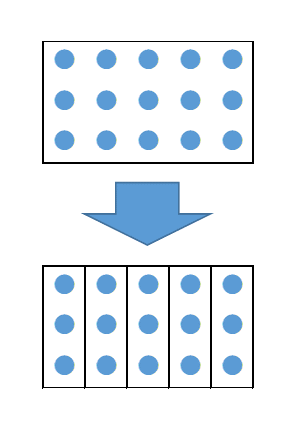
3個ずつ除いていく、と考えれば除算と呼ぶのも自然だと感じられるでしょう。また、上の図を板チョコだと思えば、3個ずつ割っていくと考えられるので、割り算と呼ぶのも自然な感じがしますね。

逆に、3人に1個ずつお菓子をあげると、5周すれば全部で15個のお菓子を配ることになります。このことから、割り算は掛け算の逆の計算を行っていることがわかります。上の図では、矢印の上から下へと見れば割り算で、下から上へと見れば掛け算になります。式で書けば、 $a\div b=q$ と $a = b \times q$ は同じことを表します。

余り

先ほどの計算で見たように、 $15$ から $3$ を何度も引くと、5回引けて、残りは $0$ です。ただ、毎回きれいに $0$ で終わるわけではありません。次のコードを見てみましょう。

#include <iostream>
using namespace std;

int main(){
  int a = 17, b = 3, q = 0;
  while (a >= b) {
    a -= b;
    q++;
  }
  cout << q << "\\n"; // 5
  cout << a; // 2
  return 0;
}

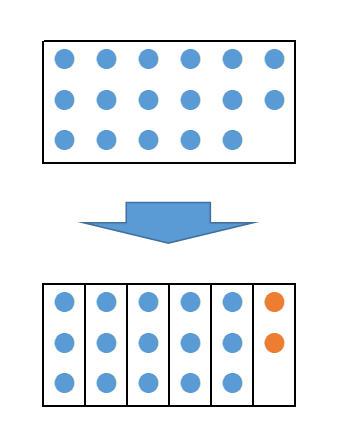
上のコードからは、 $17$ から $3$ を何度も引くと、5回引けて $2$ が残る、という結果が得られます。このように、これ以上引けなくなるまで何度も同じ数を引いた場合、最終的に残ってしまう数を、余り(remainder) といいます。上の例では、「 $17$ を $3$ で割った余りは $2$ だ」といいます。

正の整数同士の割り算で $a\div b$ の余りが $r$ であるとき、 $r$ は必ず $0$ 以上 $b-1$ 以下の整数となります。 もし $b$ 以上なら、もっと引くことができるからです。

小学校の間は、次のように3つの点で余りを表していました。\[ 17\div 3 = 5\ldots 2 \]ただ、この表記は、式変形がしにくくなることもあって、中学校以降では使わなくなります。かわりに、次のように表現するようになります。\[ 17 = 3\times 5 + 2 \]割り算と言いつつ、割り算の記号がありませんが、本質的には、商と余りを表している式になっています。

また、 $a,b$ を $p$ で割ったときの余りが等しいとき、\[ a\equiv b \pmod{p} \]と表します。少し長いですが、「 $p$ を法として、 $a$ と $b$ は合同」と読みます。

C++では、 $a\div b$ の余りは、a % bで表します。先ほどのコードは次のように書けます。

#include <iostream>
using namespace std;

int main(){
  int a = 17, b = 3;
  cout << a / b << "\\n"; // 5
  cout << a % b; // 2
  return 0;
}

ここで、1つ注意なのですが、C++では、整数同士の割り算の答えは、つねに整数になります。上のコードでは、a / bの結果は、5.66666などとはならず、小数点以降の部分は無理されて5になります。 $3$ が引ける回数が返ってくる、と考えるといいでしょう。

もし、商を小数にしたい場合は、変数を小数として宣言して計算します。つまり、double型で宣言してから計算するということです。

#include <iostream>
using namespace std;

int main(){
  double a = 17, b = 3;
  cout << a / b << "\\n"; // 5.66667
  return 0;
}

割り算の結果がどうなるかは、言語によって異なります。例えば、Pythonであれば、そのまま計算すると小数が返ってきます。C++のときのように小数点以下を無視したい場合は、// という記号を使います。

a, b = 17, 3
print(a / b) # 5.666666666666667
print(a % b) # 2
print(a // b) # 5

このように、使う言語によって小数点以下の扱いが異なるので、注意しましょう。

$a\div b$ の余りが $0$ のとき、「 $a$ は $b$ で割り切れる」とか、「 $b$ は $a$ を割り切る」といい、数学では $b\mid a$ で表します。今までの計算でいえば、15は3で割り切れ、17は3で割り切れない、ということです。記号では、 $3\mid 15$ と表します。

ここまでの内容を踏まえると、AtCoder ABC 016 A - 12月6日が解けるようになります。

負の整数の割り算

負の整数を含んだ割り算は、以下で述べるように少し面倒な点があるので、競プロではあまり登場しませんが、一応紹介しておきます。

正の整数を正の整数で割るところで見ましたが、 $a\div b = q$ と $a = b\times q$ は同じことを表します。このことを利用して、負の整数の割り算を考えます。

まずは、余りがない場合を考えます。 $-15\div 3$ は、 $3$ に何を掛ければ $-15$ になるか、と考えます。正の整数に負の整数を掛ける場合、符号のことをいったん忘れて掛け算をし、その後でマイナスにするのでした（参考：整数の掛け算）。なので、 $3$ に何を掛ければ $-15$ になるかも、符号のことをいったん忘れて計算をし、その後でマイナスをつけます。つまり、\[ -15\div 3=-5 \]と計算します。負の整数を正の整数で割るときも同じで\[ 15\div(-3)=-5 \]と計算します。

負の整数を負の整数で割る場合は、答えの符号は正になります。これも掛け算のときと同じです。\[ -15\div(-3)=5 \]となります。

余りがある場合は少しやっかいです。どのように処理するかは言語によって異なります。C++では、昔はコンパイラによって答えが異なる、という状況にもなっていました。例えば、 $-17$ を $-3$ で割ったとき、商が $5$ で余りが $-2$ とする処理もあれば、商が $6$ で余りが $1$ とする処理もありました。C++11以降は、商は必ず小数以下を切り捨てる（ $0$ に近い方に丸める）ことになっています。

負の整数を含んだ割り算でも、割り切れるときの商は信用できます。割り切れないときには、余りが $0$ でないことも確実です。これらは安心して使えます。しかし、割り切れないときに商や余りを使いたい場合は、どういう結果になるか、はっきり理解している場合以外は使わない方がいいでしょう。間違いやすいので、正の整数に変換してから後で符号の処理をする、とした方がいいと思います。

なぜ0で割ることができないか

割り算の計算では、 $0$ で割ることはできません。

冒頭で見たように、割り算を「何回引けるか数えるもの」と考えると、わかりやすいですね。何度でも引けます。無限回引けてしまうので、「割れない」と考えます。

また、割り算が掛け算の逆であることを利用して考えることもできます。例えば $3\div 0$ は「$0$ に何を掛ければ $3$ になるか」を考えることになりますが、どんな場合も $3$ にはなりません。 $0$ に何を掛けても、答えは $0$ だからです。この点からも、 $0$ では割れないことがわかります。

プログラミングの世界では、0 で割ったときの処理は言語によって異なります。エラーとなるものもあれば、意味不明な数字を返すものや、NaN(not a number のこと) を返すものもあります。割り算をするときは、割る数が $0$ でないことを確かめる必要があります。実務では場合分けをする必要がありますが、競プロでは 0 で割ることがないように入力値が調整されていることが多いです。

おわりに

ここでは、整数の割り算について見てきました。商が整数になる言語では、数学で行っていた計算とは違う結果になる可能性があり、間違いやすいので注意しましょう。