分配法則

ここでは、「和の積」が「積の和」に分解できる分配法則についてみていきます。また、この計算方法を利用して、余りの計算のところで見た、積の余りの計算方法を再度見てみることにします。

分配法則その１

次のように、縦に5個ずつ丸を並べていきます。横に4列並べ、その横に3列並べます。

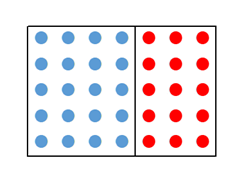
このとき、列は全部で $4+3$ 列できているので、色を無視して数えると、丸の数は $5\times(4+3)$ と表すことができます。

一方、色で分けて、4列と3列としてから丸の数を数えるとすると、丸の数は $5\times 4 + 5\times 3$ と表すことができます。

まとめて数えても分けて数えても答えが変わるはずはないので、\[ 5\times(4+3) = 5\times 4 + 5\times 3 \]が成り立ちます。同じような図を用いて考えれば、縦の数や横の数を変えても、同様の式がなりたつことがわかるでしょう。つまり、正の整数 $a,x,y$ について、次の式が成り立ちます。（実は、負の整数や小数でも成り立ちます）\[ a(x+y) = ax+ay \]$a(x+y)$ は、 $a$ と $(x+y)$ との積ということです。掛け算記号が省略されています。

手計算で行うときは、 $a$ が $x,y$ の両方に掛けられていると考えて変形します。

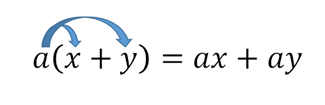
$y$ にも $a$ を掛ける必要があります。これを掛け忘れる間違いが多いので注意しましょう。

分配法則その２

次のように、縦に7個ずつ丸を並べていきます。横に4列並べ、その横に3列並べます。さらに、縦を5個と2個に分けてみます。

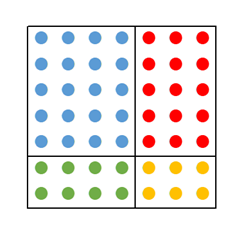
このとき、色を区別しなければ、丸の数は $(5+2)\times(4+3)$ と表すことができます。先ほどと同じように分解すると、この式はどうなるでしょうか。

まず、縦に $(5+2)$ 個並べることは固定して、列を4列と3列に分けると考えてみます。そうすると、次のような式に変形できます。\[ (5+2)\times 4+(5+2)\times 3 \]先ほどの「その１」で見たときと同じような分解の仕方です。 $(5+2)$ がひとつのかたまりだと考えています。青・緑と、赤・オレンジをひとかたまりだと考えている、ということです。

次にそれぞれを分解しましょう。縦に並べる数を $5,2$ で分けるとすると、4列の部分は\[ (5+2)\times 4=5\times 4+2\times 4 \]と変形することができます。3列の方も同じように変形できます。

以上から、 $(5+2)\times(4+3)$ は、次のように分解して計算することができます。\[ 5\times 4+2\times 4+5\times 3+2\times 3 \]この内容は一般的な場合でも成り立ちます、正の整数 $a,b,x,y$ について、次の式が成り立ちます（負の整数や小数でも成り立ちます）。足し算の順番を変えていますが、足し算は順番を変えても答えが同じなので問題ありません。\[ (a+b)(x+y) = ax+ay+bx+by \]手計算で行うときは、 $a,b$ が $x,y$ のそれぞれに掛けられていると考えて、変形します。

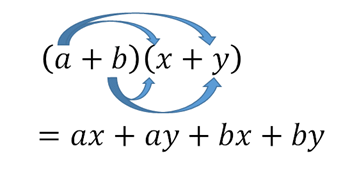
4つの掛け算が出てきますが、これは先ほどの図で4つの領域ができることに対応しています。

ここでは、次のような計算が成り立つことを見ました。
\begin{eqnarray}
a(x+y) &=& ax+ay \\[5pt]
(a+b)x &=& ax+bx \\[5pt]
(a+b)(x+y) &=& ax+ay+bx+by
\end{eqnarray}

このような計算ルールを、分配法則(distributive law) といいます。この計算はいろんなところで使われます。その一例として、積の余りの計算での応用を見てみます。

分配法則と積の余り

余りの計算のところでは、 $a,b$ の積を $p$ で割った余りは、それぞれの余りの積を $p$ で割った余りに等しいことを見ました。これを分配法則を使って確かめることができます。

正の整数 $a,b$ を、正の整数 $p$ で割るとします。それぞれ、商が $q_a,q_b$ で、余りが $r_a, r_b$ であったとしましょう。つまり、次の式が成り立つということです（参考：整数の割り算）。\[ a=pq_a+r_a,\ b=pq_b+r_b \]このとき、 $a,b$ の積は、分配法則を使って、次のように変形できます。
\begin{eqnarray}
ab
&=&
(pq_a+r_a)(pq_b+r_b) \\[5pt]
&=&
p^2q_aq_b+pr_aq_b+pq_ar_b+r_ar_b \\[5pt]
\end{eqnarray}文字が多くて複雑な感じがしますが、よく見てみるといいことが起こっています。はじめの3つには、 $p$ が掛けられています。そのため、はじめの3つは、 $p$ で割り切れることがわかります。このことは、 $ab$ を $p$ で割った余りが、 $r_ar_b$ を $p$ で割った余りに等しいことを表しています。 $r_a, r_b$ は余りを表していたから、結局、 $a,b$ の積を $p$ で割った余りは、それぞれの余りの積を $p$ で割った余りに等しいことが確かめられました。

式でまとめると\[ ab\equiv r_ar_b \pmod p \]となることが、分配法則を使って示せたことになります。

因数分解

$a(x+y)=ax+ay$ という変形を分配法則ということを見ました。これは、左から右への変形とみることもできますが、右から左へ変形することにも使えます。

そんな変形をして何がいいのかというと、例えば倍数についての情報がわかりやすくなります。例えば、先ほどの計算で、\[ p^2q_aq_b+pr_aq_b+pq_ar_b+r_ar_b \]という式が出てきました。このうち、初めの3つには $p$ が掛けられているから、初めの3つは $p$ の倍数だ、と書きましたが、次のように変形するとそれがよりわかります。\[ p(pq_aq_b+r_aq_b+q_ar_b)+r_ar_b \]分配法則を使って元に戻せば、同じ式であることがわかります。こうすると、前の3つは、 $p$ と整数の積であり、 $p$ の倍数になっていることがわかりやすいですね。

このように、 $ax+ay$ を $a(x+y)$ と変形することを因数分解(factorization) といいます。因数分解の計算はいろいろなバージョンがありますが、まずはこの変形を知っておきましょう。

分配法則と筆算

「分配法則」と難しそうな名前がついていますが、考え方はだいぶ前に登場しています。小学校3年で習う、2桁同士の掛け算でも使われています。

2桁同士の掛け算では、筆算を使って次のような計算をします。
\begin{array}{r}
23 \\
\times \ 45 \\
\hline
115 \\[0pt]
\ 92\color{White}{0} \\[0pt]
\hline
1035 \\
\end{array}5行あるうち、3行目は $23\times 5$ を行っています。4行目は右端が空欄です。省略されていますが、ここには本来 $0$ が入るべきで、4行目は $23\times 40$ の計算をしていることになっています。つまり、45を、5と40に分けて、\[ 23\times (5+40) =23\times 5 +23\times 40 \]というふうに分解して計算していることになります。筆算の3行目が前半の掛け算に、4行目が後半の掛け算に対応し、5行目がこの2つの和の計算に対応しています。この式は、分配法則を使った式と同じ形です。

分配法則という言葉は出てきませんが、和を分解して掛け算行う手法・考え方は、こんな昔から扱っていたんですね。

おわりに

ここでは、分配法則について見てきました。また、途中で因数分解についても触れました。競プロでは、何を計算すればいいかを考える際に、こうした式変形を使うことがあるので、計算方法を知っておいた方がいいでしょう。

数学の内容として学びたい場合は、中学生向けの記事ですが、【基本】正負の数と分配法則が役に立つと思います。高校生向けの記事では、少し複雑になりますが、【基本】整式の乗法 や 【基本】展開の公式などが参考になるでしょう。