🕒 2019/11/15 🔄 2024/10/16

組合せ

🗼

ここでは、異なるものからいくつかを選ぶ方法を数えていきます。

📘 目次

組合せ

順列では、 $N$ 個の異なるものから $K$ 個を選んで一列に並べる方法の総数を考えました。ここでは、並べずにただ選ぶだけの場合を考えてみます。

並べる操作が減るので簡単になるような気がするんですが、並べなくなることで少し面倒なことが起きてしまいます。樹形図を使うとダブってしまうものがでてきてしまいます。

例えば、1, 2, 3, 4 から2つの数字を選ぶ方法を考えましょう。樹形図を使えば、次のようになるような気がします。

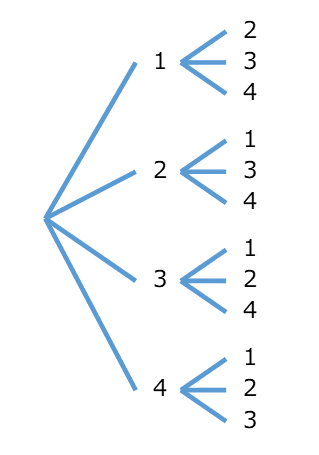
しかし、今の場合、これだと同じものを重複して数えてしまっています。例えば、「2, 4」と選んだのと「4, 2」と選ぶのとでは、同じ選び方です。並べるときは1番目と2番目は別物ですが、選ぶだけなら1番目と2番目の違いはないので、このままだと二重に数えてしまうことになります。

上の樹形図では、「○□」と「□○」は、同じ選び方なのに2回ずつ数えていることになるので、選び方の総数は\[ \frac{4\times 3}{2} \]通り、つまり、6通りとなります。

では、1, 2, 3, 4 から3つの数字を選ぶ方法だとどうなるでしょうか。この場合も樹形図を使って考えると、一つの組合せをダブってカウントしていることになります。今回は、それぞれの組合せを何回ダブって数えているでしょうか。先ほどの流れから3回と予想する人もいるかもしれませんが、実際にはもっとダブって数えてしまっています。

「○△□」と同じ選び方になるのは、以下の通りです。

○△□
　○□△
　△○□
　△□○
　□○△
　□△○

つまり、樹形図を使って数えると、1つの組合せを6回もダブってカウントしていることになります。これは、3つの異なるものを並べた順列の総数なので、 $3!$ 回と書くこともできますね。この $3!$ 回を1通りと数えないといけないので、選び方の総数は\[ \dfrac{4\times 3\times 2}{3\times 2\times 1} \]通りとなります。つまり、4通りです。

一般に、 $n$ 個の異なるものから $k$ 個を選ぶ組合せの総数は、 ${}_n\mathrm{C}_k$ で表します。これは次のように計算できます。\[ \frac{n(n-1)\cdots(n-k+1)}{k(k-1)\cdots 1} \]分母も分子も、 $k$ 個の数の積です。分子は、 $n$ 個の異なるものから $k$ 個を取り出して一列に並べる場合の数です。これを、「 $k$ 個の異なるものを一列に並べる場合の数」で割っています。それぞれの組合せをこれだけの回数だけダブって数えているので、このように割る必要があります。

この式を ${}_n\mathrm{P}_k$ を使って表すと、先ほどの分子がこの式と同じなので、\[ {}_n\mathrm{C}_k=\dfrac{ {}_n\mathrm{P}_k}{k!} \]とかくことができます。さらに、 ${}_n\mathrm{P}_k$ も階乗を使って表すと\[{}_n\mathrm{C}_k=\dfrac{n!}{k!(n-k)!}\]となります。例えば、 $n=4, k=3$ なら、\[{}_4\mathrm{C}_3=\dfrac{4!}{3!(4-3)!}=\dfrac{24}{6\cdot 1}=4\]なので、4通り、と計算できます。

組合せの総数をコードで求める

$n$ 個の異なるものから $k$ 個を選ぶ組合せの総数を求めるコードをかいてみます。つまり、 ${}_n \mathrm{C} _k$ を求めるということです。条件は、 $1\leqq k \leqq n \leqq 12$ とします。なお、 $12!$ は int型におさまるので、この条件下では int型内で計算できます。

コードでは階乗を計算するのは簡単なので、階乗を使った式 $\dfrac{n!}{k!(n-k)!}$ をコードにすることを考えます。

$n!$, $k!$, $(n-k)!$ の3つの階乗が計算できればいいですね。階乗は、和や階乗と再帰関数で再帰関数を用いた書き方を見たので、ここでは for文を使う方法で書いてみます。

#include <iostream>
using namespace std;

int factorial(int n) {
  int ans = 1;
  for(int i = 1; i <= n; i++) {
    ans *= i;
  }
  return ans;
}

int main() {
  int n, k;
  cin >> n >> k;
  cout << factorial(n) / factorial(k) / factorial(n - k);
  return 0;
}

$\dfrac{n!}{k!(n-k)!}$ をコードで表しています。factorial は階乗を返す関数です。

ところで、 $\dfrac{n!}{k!(n-k)!}$ という式を見ると、割り切れるかどうかはパッとはわかりにくいですね。しかし、これは「 $n$ 個の異なるものから $k$ 個を選ぶ組合せの総数」を表しているので、正の整数になることが決まっています。int型で計算しているから整数になっているのではなく、本当に割り切れて整数になります。少し不思議ですね。

同じものを含む順列

順列では、異なるものからいくつかを選んで一列に並べる方法の総数を考えました。また、このページでは、異なるものからいくつかを選ぶ組合せの総数を考えました。

ここで数え方の注意点なのですが、「並べる場合は ${n}\mathrm{P}_k$ で、組合せなら ${n}\mathrm{C}_k$ を使う」という覚え方をしてはいけません。順列と組合せで大事なことは、(1) 樹形図をかいたときに、同じ構造をまとめて数えること、(2) 何度もダブって数えている場合は、ダブっている回数で割ること、この2つです。

これを踏まえて、同じものを含む順列を考えてみます。

●,●,□,□ の4つの文字を横一列に並べるとき、並べ方の総数はどうなるでしょうか。

単純に掛け算をして求めることはできません。1文字目の決め方は●か□かの2通り、2文字目も2通りですが、3文字目は2通りかどうかはわかりません。1文字目と2文字目で●を使っていたら、3文字目は□で確定してしまうからです。同じものが含まれている場合は、すべて異なっている場合とは違った数え方をしなくてはいけません。

対応策として、一旦区別してから数える、という方法があります。とりあえず、 A, B, C, D という名前をふり、この4文字を並び替えます。その後で、A, B は●に、C, D は□に置き換える、という数え方です。

こうすると、4つの文字の並べ方は $4!$ 通りです。その中で、A, B を●にするため、並べ方のうち A が先に来ていたものと B が先に来ていたものは、2回ダブって数えていることがわかります。 C, D も同様です。そのため、ダブって数えていた回数で割って、\[ \dfrac{4!}{2!2!} \]通りだ、と求められます。

別の考え方として、何番目に並べるかを考える、という発想もあります。4つの場所に ●,●,□,□ を置くとして、●を何番目と何番目に置くか、と考えます。これは、4つの場所から、●を置く2か所を選ぶ、と考えられるので、 ${}_4\mathrm{C}_2$ 通りとなります。1つ目の方法と同じ答えになります。

2つ目の考え方は、このページの一番はじめの例（1, 2, 3, 4 から2つ選ぶ方法）と、同じものを数えていることになります。見た目はまったく異なりますけどね。このように、数学の問題でも、競プロの問題でも、場合の数に関する問題では、数えやすいまったく別の問題に変換して数えることも多く、柔軟な発想が求められます。

おわりに

ここでは、組合せの総数を考える上で基本的となるものを見てきました。実際の競プロの問題ではもっと大きな数を扱うのですが、そのためには計算方法について見る必要があります。今後、見ていくことになります。

なお、数学の内容として学びたい場合は、【基本】組合せやその関連ページが役に立つでしょう。