🕒 2020/05/02 🔄 2024/10/14

第二回アルゴリズム実技検定 N - ビルの建設解説

🐻

問題

問題概要

2次元平面上に、各辺が x, y 軸に平行な正方形の敷地が $N$ 個あります。 $i$ 個目の敷地は、領域 $x_i\leqq x \leqq x_i + D_i$, $y_i\leqq y \leqq y_i+D_i$ であり、各敷地にはコスト $C_i$ が定まっています。

今、 $Q$ 件のビル建設計画があり、 $j$ 件目の計画での建設予定地は $(A_j, B_j)$ です。各計画のコストは、その計画の建設座標を含む（境界線上にある場合も含む）すべての敷地のコストの和です。

各計画のコストを求めてください。

制約

$1\leqq N \leqq 50000$
$1\leqq Q \leqq 100000$
$-10^9\leqq x_i, y_i \leqq 10^9$
$1\leqq D_i \leqq 10^9$
$1\leqq C_i \leqq 10^9$
$-10^9\leqq A_i, B_i \leqq 10^9$
入力はすべて整数

解説

例えば、リンク先の入力例2を見てみましょう。左下の点が $(-3,5)$ で一辺が $4$ の正方形と、左下の点が $(1,9)$ で一辺が $7$ の正方形、合計2つの敷地があるという状況です。コストはそれぞれ $100$ と $30$ です。

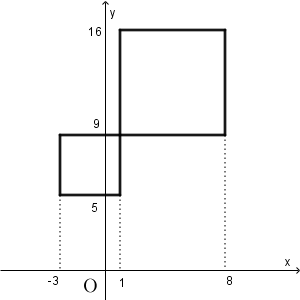
このとき、建設予定地が $(1,9)$ の場合は、2つの正方形の頂点上にあり、領域内だから、コストは $130$ になります。 $(1,8)$ の場合は1つ目の正方形の境界線上にあって領域内だから、コストは $100$ になります。 $(8,10)$ の場合は、2つ目の正方形の内部にあるので、コストは $30$ です。

やること自体は単純です。愚直にやるなら、各建設予定地に対して、各正方形に入っていればコストを足す、というのを繰り返していけばいいですね。しかし、それでは間に合いません。この方法では $O(NQ)$ の時間がかかり、時間内に計算できません。

そこで、制約を見つつ、間に合うように計算するにはどうすればいいかを考えます。敷地の左下の頂点も、建設予定地の場所も、 $-10^9$ 以上 $10^9$ 以下の広い領域内にあるので、これは利用できなさそうです（もっと小さければ、各点のコストを全部計算しておくとかができるかもしれませんが）。 $C_i$ も大きな値をとりうるので、コストから攻めるのもなかなか難しそうです。

小さな値は $N,Q$ しかないので、これらを利用する方法しかなさそうです。この視点で考えつつ、「領域が広くて扱いにくい」ことも合わせると、実は領域全体を考える必要がないことに気づきます。先ほどの例でいえば、 $x$ 座標については、 $x=-3,1,8$ が重要で、他の $x$ 座標はたいして重要でないことがわかります。

ざっくりいえば、 $2\times 10^9+1$ 個あった $x$ 座標のうち $2N$ 個程度の座標に注目すればよさそうです。 $y$ 座標についても同様です。つまり、正方形の辺を含む直線だけに注目すればよさそう、ということです。

重要な点はわかったものの、ここからどうやって各計画のコストを計算すればいいでしょうか。いきなり2次元で考えるのは大変なので、1次元の場合で考えてみます。

例えば、上のような3つの区間があって、区間の内部に点があったら、各数字が足されるとしましょう。例えば、 $x=3$ の場合は、1つ目と3つ目に入っているので、 $60$ になる、という具合です。 $x=9$ なら、3つ目だけに入っているので $10$ です。

これの区間の両端だけに注目して管理できるようにするには、区間の端で数字を足すようにすればいいでしょう。

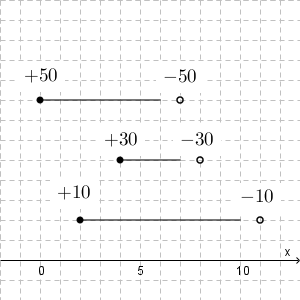
「点が区間に入っていたら $+50$ する」というのを、「点が区間の左端か超えていたら $+50$ して、右端を超えたら $-50$ する」というように変えています。右端が1個飛んでるのは、区間の右端に入っていたときも数字を加算するためです。このように管理すれば、区間の端だけを見ることで、コストを効率的に計算できるようになります。例えば、 $x=3$ の場合は、 $x=0,2$ の部分で数字が加算されて $60$ になり、 $x=9$ なら、 $+50+10+30-50-30$ となって、 $10$ となります。

そうすると、今後は「列に値を足したり、累積和を効率的に計算する方法」が必要になりますが、これにはBIT（Binary indexed tree）が使えます。BITについては、Binary indexed treeやBinary Indexed Tree のはなし(PDF)がわかりやすいです。

今の問題は2次元なので、2次元BITを使います。正方形の左下の点を $(x_i,y_i)$ とし、一辺の長さを $D_i$, コストを $C_i$ とすると、先ほどの区間の例で見た通り、 $(x_i,y_i)$ で $C_i$ を足し、 $(x_i+D_i+1,y_i)$ で $C_i$ を引きます。2次元の場合は、上側も処理しないとダメで、 $(x_i, y_i+D_i+1)$ で $C_i$ を引きます。こうすると右上の部分の処理も必要となり、 $(x_i+D_i+1,y_i+D_i+1)$ で $C_i$ を足さないといけません。これで1つの正方形の処理が終わります。

各計画地でのコストは、BITを使った累積和で求められます。以上から、C++で書くと、次のようになります。コードの下にコードの説明が続きます。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;

template <typename T>
struct BIT2D {
  int X, Y;
  vector<vector<T>> bit;
  BIT2D(int X_, int Y_) : X(X_ + 1), Y(Y_ + 1) {
    bit.assign(X, vector<T>(Y, 0));
  }

  void add(int x, int y, T a) {
    for (ll i = x; i < X; i += (i & -i)) {
      for (ll j = y; j < Y; j += (j & -j)) {
        bit[i][j] += a;
      }
    }
  }

  T sum(int x, int y) {
    T ans = 0;
    for (ll i = x; i > 0; i -= (i & -i)) {
      for (ll j = y; j > 0; j -= (j & -j)) {
        ans += bit[i][j];
      }
    }
    return ans;
  }
};


int main() {

  ll N, Q; cin >> N >> Q;

  vector<ll> X(N * 2), Y(N * 2), D(N), C(N);
  vector<ll> XI(N * 2), YI(N * 2);
  BIT2D<ll> bit(N * 2, N * 2);

  for (ll i = 0; i < N; i++) {
    cin >> X[i] >> Y[i] >> D[i] >> C[i];
    X[i + N] = X[i] + D[i] + 1;
    Y[i + N] = Y[i] + D[i] + 1;
  }
  XI = X, YI = Y;
  sort(XI.begin(), XI.end());
  sort(YI.begin(), YI.end());
  XI.erase(unique(XI.begin(), XI.end()), XI.end());
  YI.erase(unique(YI.begin(), YI.end()), YI.end());

  for (ll i = 0; i < N; i++) {
    ll xi1 = lower_bound(XI.begin(), XI.end(), X[i + 0]) - XI.begin();
    ll xi2 = lower_bound(XI.begin(), XI.end(), X[i + N]) - XI.begin();
    ll yi1 = lower_bound(YI.begin(), YI.end(), Y[i + 0]) - YI.begin();
    ll yi2 = lower_bound(YI.begin(), YI.end(), Y[i + N]) - YI.begin();
    xi1++, xi2++, yi1++; yi2++;

    bit.add(xi1, yi1,  C[i]);
    bit.add(xi1, yi2, -C[i]);
    bit.add(xi2, yi1, -C[i]);
    bit.add(xi2, yi2,  C[i]);
  }

  vector<ll> ans(Q, 0);
  for (ll i = 0; i < Q; i++) {
    ll x, y; cin >> x >> y;
    ll xi = upper_bound(XI.begin(), XI.end(), x) - XI.begin();
    ll yi = upper_bound(YI.begin(), YI.end(), y) - YI.begin();
    cout << bit.sum(xi, yi) << '\\n';
  }

  return 0;
}

前半は一般的な2次元BITの処理です。 main では、まず、 $x$ 座標と $y$ 座標のうち、値の更新に使うものだけを抽出しています。左・下の $x_i,y_i$ と右・上の $x_i+D_i+1,y_i+D_i+1$ を集め、ソートして重複を消しています。いわゆる、座標圧縮です。コストの計算では正方形の境界を含むので、 $x_i+D_i$ ではなく $x_i+D_i+1$ である点に注意です。

次に、変化点の更新です。正方形の辺に来たらコストを足し引きする処理を行っています。最後に、コストの計算です。境界線上での計算が正しくできるように upper_bound を使っています。 lower_bound だと、正方形の処理をする前にコストを計算することになってしまうため、点が境界線上にあるときにうまく計算できません。

第二回 アルゴリズム実技検定 N - ビルの建設 解説

問題

問題概要

制約

解説

第二回アルゴリズム実技検定 N - ビルの建設解説