なかけんの競プロノート
🕒 2021/02/14 🔄 2021/06/14

ARC112感想戦

🐺

AtCoder Regular Contest 112 に参加しました。結果は、ABが解けてCが解けず、D以降は見てもない、です。画像はコンテスト中に書いたメモです。

Aは、LとRが与えられるので、L以上R以下の3つの整数 A, B, C の組で、 A-B=C を満たすものの個数を答える問題。「B=C」という問題文だけど、タイトルは「A-B=C」となるのね。

これ、結構悩んでしまった。まず初めに考えたのは、それぞれLを引いてから考えたほうがいいかな、ということ。A'=A-L、B'=B-L、C'=C-L と置けば、0以上、R-L以下の整数を考えればいい、となる。また、条件式 A-B=C は、代入して整理すると、A'=B'+C'+L となる。これを満たすとき、 A'は必ず0以上になる。B'とC'が0以上であり、B'+C'+L が R-L 以下となる場合を考えると、B'とC'はR-L以下となる。

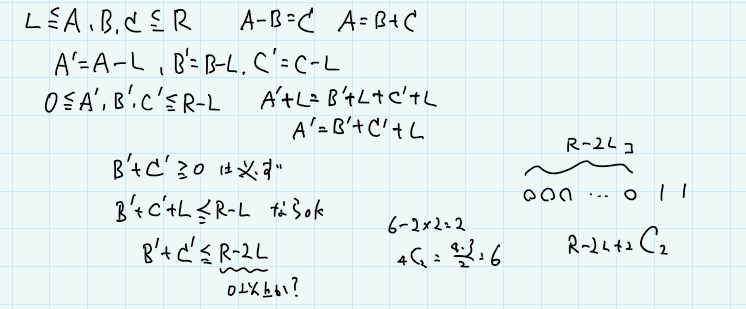
なので、B', C'がどちらも0以上で、 B'+C'+LがR-L以下となる組を数えればいい（このとき、自動的に条件を満たすA'も作れるから）。結局、B'+C'がR-2L以下となる組を数えればよく、これは、〇をR-2L個と | を2個を並び替える場合の数に等しい（一つ目の線の左側の〇の数をB'、二本の線の間の〇の数をC'とすればいい）ので、 ${}_{R-2L+2}\\mathrm{C}_2$ を計算すればいい。 $R-2L$ が負なら、組の数は $0$ にすればいい。

おーこれでO(1)になるのか。しかもやることは $(R-2L+2)(R-2L+1)/2$ を計算するだけなので簡単。しかし、時間はめっちゃかかった（15分）。通した後に順位表を見たら、1500位くらい。え、もっと楽に解けるの？　ヤバい予感しかしない。

Bは、与えられた整数に対して、「1円はらってマイナス1を掛ける」や「2円払って1を引く」を好きなだけ繰り返す。C円以内で、最終的に得られる整数の種類を答える問題。

処理は途中でやめてもいいので、左端と右端の限界値を考えればいい。例えば、はじめが正の整数の場合、答えも正の整数のままできる限り大きくするには、「-1を掛けて1をできる限り引いて、最後に-1を掛ける」で、小さくするには「-1をできる限り引く」。もしマイナスになってしまったら左端の限界は1と考えることにする。答えを負の場合にしたいときも同じように考え、0にもできる場合は最後に1個足す。

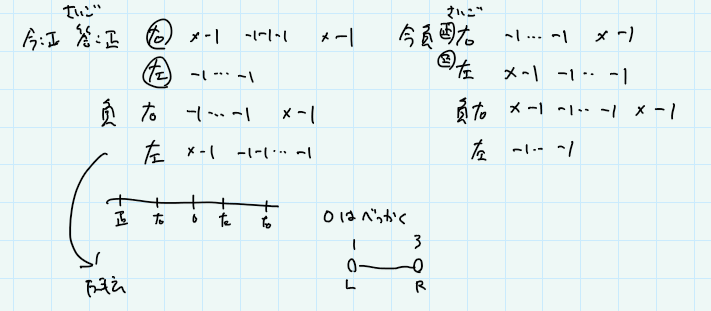
これを、負の整数がスタートのとき、0がスタートのときにわけ、さらにはじめのお金が1円のときも場合分け（これはスタートの整数が0かそれ以外かでさらに場合分け）する。

うーん、こんなに場合分けをしまくるのだろうか、と考えつつも、やる。ミスってそうだけど、なんとか1回でAC。（ここまでで59分）

Cはゲームの問題。実験してみると、ある点から下に伸びる深さによって、選手交代が起きたり起きなかったりするので、それを計算するんだろうと思いつつ、結局どうやればいいかわからず。コードは何もかけないまま終了。