なかけんの競プロノート
🕒 2021/01/31 🔄 2021/06/14

ABC190感想戦

👓

AtCoder Beginner Contest 190 に参加しました。結果は、Dまで解けて、Eは格闘したものの解けず。画像はコンテスト中に書いたメモです。

Aは、書いてみたもののあまり自信がなくて、恐る恐る提出。いつもより慎重めにやったので、ちと遅かった。ここまで3分。

Bは、1個1個チェックしていけばいいだけ。ここまでで6分。

Cは、すべてのケースをチェックしていくだけ。ただ、入力処理をミスっていて（ $A_1,B_1,A_2,B_1,\\cdots$ ではなく $A_1,A_2,A_3,\\cdots$, $B_1,B_2, B_3,\\cdots$ だと思ってた）時間をロスしてしまった。ここまでで13分。

Dは、Nが与えられるので、整数からなる公差1の等差数列で総和が N になるものの個数を求める問題。

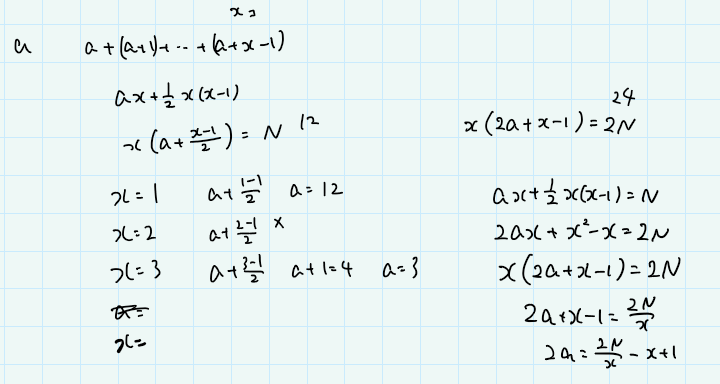
初項を $a$ と置いて、項の数を $x$ とおくと、 $a$ から $a+x-1$ までの整数の和が $N$ 、という条件になる。この和は、 $a$ が $x$ 個と、 $0$ から $x-1$ までの和なので、\\[ ax+\\dfrac{x(x-1)}{2}=N \\]と変形できる。さらに変形すれば、\\[ 2a=\\frac{2N}{x}-x+1 \\]となる。

なので、 $1\\leqq x\\leqq \\sqrt{2N}$ に対して $\\dfrac{2N}{x}$ が整数のときに、先ほどの式を満たす整数 $a$ があるかどうかを判定していけばいい。ここまでで23分。

Eは、隣り合わせにできる石の組が複数与えられるので、指定した石を含む列が作れるかどうかを判定する問題。作れる場合は長さも答える。

まず、隣り合わせにできるかどうか、をグラフで表現して考えるのはすぐに思いついた。あと両端は指定された石のどれかになることもわかる。

$K$ の数（指定された石の数）は小さいけど、それをどうやって生かすかがなかなかわからず。でも、途中で巡回セールスマン問題であることを思いつく。

$C_i$ から出発したときの最短距離を計算しないとダメだな、という気持ちと、指定された石を含む部分が連結になってないとダメだな、という気持ちもわいてきた（後者は実は考えなくてもよかったんだが）。それで結局、

  • 連結かどうか（連結じゃなかったら即 -1 を返して終わり）
  • $C_i$ から出発したとときの各石への最短距離をそれぞれ計算
  • $C_i$ たちを使って巡回セールスマン問題を解く

という流れで書くことにしたんだけど、最後の部分ができず。前も、巡回セールスマン問題ができなかったような。

Fも問題を見たのだけど、転倒数はあまり解いてなくて避けた。しかし、途中で解いている人の数を見て、「いやこっちに力を振っておくべきだったか」という気にもなった。しかし、結構時間を使った後に、いまさらFにつっこむのもなぁ、と思って、レートは少し下がっておしまいという結果に。