なかけんの競プロノート
🕒 2021/01/24 🔄 2021/06/14

ABC189感想戦

🧦

AtCoder Beginner Contest 189 に参加しました。結果は、Eまで解けて、Fは格闘したものの解けず。画像はコンテスト中に書いたメモです。

Aは、3文字がすべて同じ文字かを判定するので、そのまま調べればOK。1分。

Bは、アルコール度数が $P_i$ %のお酒を $V_i$ ml 飲んだ時に、アルコール摂取量が $X$ ml を超えたのは $N$ 杯のお酒のどのタイミングか、を答える問題。%をそのまま計算すると小数が出てきて誤差が発生するので、すべての値を100倍して考えるとOK。 $V_iP_i$ の和が $100X$ を超えるタイミングを計算すればいい。ここまでで3分。

C。正の整数からなる数列があって、$\\ell$ 番目から $r$ 番目の最小値を $x$ としたときに、 $x(r-l+1)$ を計算して、これがいつ最大になるかを考える問題。

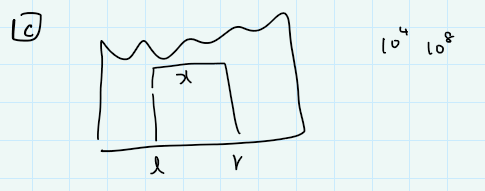
整数の大きさ $N$ が最大 $10^4$ なので、 $\\ell$ と $r$ の選び方は $N^2$ のオーダーだから、ちょっと間に合うか微妙じゃないかな、と心配に。しかし、「時間に余裕があるのかな？」と思って見てみると、1.5sec。え？ $N^2$ 通らないのかな、ひょっとして。。。という気持ちに。

そこで、もう少し早くやる方法があるのかなと思ったんだけど、パッとは思いつかなかったし、単純処理だからそんなに時間がかからないだろうという予想と、 $r$ は $\\ell$ 以上にすれば、厳密には1億回にはならないから大丈夫そうかなという予想と、C問題でそんなに難しい問題は出ないだろうという予想を合わせて、愚直に $O(N^2)$ の解法で恐る恐る提出してみる。するとAC。悩まなくてもよかったのか、、、という気持ちに。ここまでで9分。

D。 $N$ 個の文字列が与えられる。各文字 $S_i$ は AND か OR。

True か False のどちらかの値から構成される組 $(x_0, \\cdots ,x_N)$ のうち、

  • $y_0=x_0$
  • $S_i$ がANDなら $y_i=y_{i-1} \\land x_i$ 、ORなら $y_i=y_{i-1} \\lor x_i$

としたときに $y_N$ がTrueとなるものの個数を求める問題。

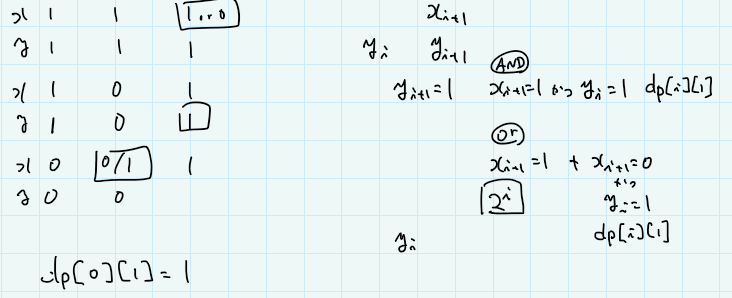
見るからにDPを使うぽいな、という印象。とりあえずサンプルを分解して考えてみる。この時点では、「 $i$ 番目まで見たときに、 $y_i$ が False の組の数と True の組の数」を計算していけばいいのかな、と思っていた（ので、dp[i][0 or 1] を考えると思っていた）。

$S_{i+1}$ がANDなら、 $y_{i+1}$ がTrueになるには、$x_{i+1}$ も $y_{i}$ もTrueじゃないといけないので、 dp[i+1][1]=dp[i][1] が成り立ちます。

一方、ORの場合は、 $x_{i+1}$ がTrueなら $i$ 番目までの結果は何でもいいので、 $x_i$ までは好きな値をとれます。なので、 $2^i$ 通りです。 $x_{i+1}$ が Falseなら $y_i$ は True じゃないといけない。ということで、dp[i+1][1]=2^i+dp[i][1]となります。

これを順番に計算していけばよくて、そもそも「 $y_i$ が Falseになる組」は計算しなくてよいことがわかったので、実装時は1次元にしました（提出 #19612816）。ここまでで26分。

Eは、平面上に $N$ 個の駒があって、 $M$ 個の操作をする。このとき、 $Q$ 個のクエリに答える。各クエリは、「 $A_i$ 回目の操作の後に $B_i$ 番目の駒はどこにあるか？」。 $M$ 個の操作は、以下の4種類のどれか。

  • すべての駒を原点を中心に時計回りに90度回転
  • すべての駒を原点を中心に反時計回りに90度回転
  • すべての駒を、直線 $x=p_i$ について対称移動
  • すべての駒を、直線 $y=p_i$ について対称移動

とりあえず、点 $(x,y)$ が操作によってどういう点に移るかを考えてみました。

対称移動は、 $\\dfrac{x+X}{2}=p$ を解いて、 $X=2p-x$ として考えました。

うーん、これは行列くさいな、と思って、回転と平行移動に分ければいいのかなと思い、行列表現に書き換えてみました。

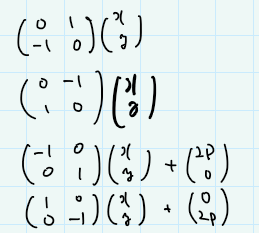
こうすると、行列の掛け算・足し算を繰り返していけばよくて、各計算結果を保持していけば、各クエリに対して答えをすぐに出せるなぁ、と思いました。

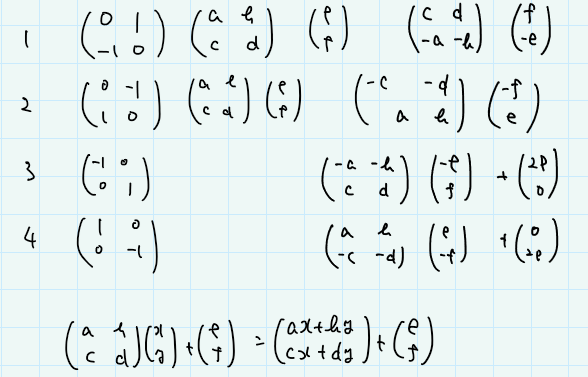
それまでの計算結果のうち、回転要素（ $a,b,c,d$ ）と平行移動要素（ $e,f$ ）について、操作によってどう変換されるかを計算し、各結果を格納していきます。最後、各クエリについて、最初の場所 $(x,y)$ がどのように変換されるかは、行列の掛け算・足し算で一発で求められます。

これをそのまま実装しました（提出 #19627200）。ここまでで51分。順位表を見ても、結構上の方だったので、かなり調子がいい感じでした。

F。0からNまでのマスがあって、すごろくをやる。１からMまでの整数が等確率で出るルーレットを回して進めていく。N以上になればゴール。ただし、途中のK個のマスのどれかに止まってしまうと「振り出しに戻る」。

このとき、ルーレットを回す回数の期待値を計算する問題。

今、 $x$ にいるとすると、期待値 $E[x]$ は、そこから1回で行けるところの期待値を全部足してMで割ったものに1を足した答えと一致します。つまり、\\[ E[x] = \\sum_{k=1}^M \\frac{1}{M}(1+E[x+k]) = 1+\\frac{1}{M} \\sum_{k=1}^M E[x+k] \\]$E[N]=0$ だし、 $N$ 以上は全部 $0$ なので、後ろから計算していけばOK。

ただ、やっかいなのは、$E[0]$ がわからない上に、「振り出しに戻る」のマスに止まったときの期待値は $E[0]$ なので、循環してしまうことなんですよね。

コンテスト中は、これは二分探索すれば出るんじゃないかと思って実装しました。しかし、サンプル4が合わず、そもそもサンプル3が収束して答えが出てしまっていました。「解法がおかしい」のか「実装がおかしい」のかわからず、別の書き方をしてみたり格闘していたのですが、結局通せず（提出 #19642390）。

コンテスト後、解法を見てみたら、解説と同じ解法が載っている。解法は間違ってなかったのかぁ、と思って実装をよくよく見返してみると、累積和の出し方がミスっていた。。。死亡。そこを修正し、少し高速化したら通りました（提出 #19650914）。

ひょっとしたらFも通せていたかもしれなかったので、これは悲しいですね。しかし、Eまで順調に通せたので、レートはかなり上がりました。

黄パフォはかなり珍しい。