ARC108感想戦
AtCoder Regular Contest 108 に参加しました。画像はコンテスト中に書いたメモです。
Aは、与えられたSとPに対して、和がSで積がPになるような正の整数2つの組が存在するかどうか答える問題。S, Pが $10^{12}$ までなので、とりあえず積の方から考えるとチェックすべき数が減る。 $10^6$ 個調べればいいので提出。が、不等号の等号を入れ忘れて1WA。はじめから嫌な予感しかしない。
Bは、文字列が与えられるので、「fox」と続いているところを消して詰める、を繰り返して、最初の文字列が最短で何文字になるかを答える問題。
はじめ、このように考えてた。まず、foxと続いているところを探す。そして、その前後が「f-ox」となっているか「fo-x」となっていたら、さらにその前後を探す、…と繰り返していく、と。
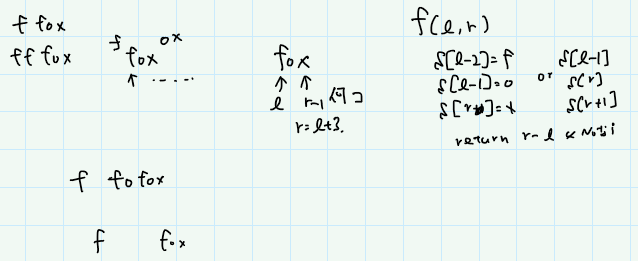
この方針でやれば行けると思って書いてみたけどWA。その後も格闘した(提出 #18267062)が通らず。
よく考えたら、この方針だと「f fox o fox x」の場合がうまくいかない。このケースに気づいてなかった(気づいたのは終わった後)。
通らなかったので、方針を変えて、stackを使って書き直す。しかし、これもWA(提出 #18268908)。これは書き方を一部ミスってたものの、方針としてはあってたんだけど、コンテスト中はもうこれは捨てるしかないと思って絶望する。
他の問題を見ると、CよりはDの方がまだ考えやすそう。文字列を扱うBができてないのに同じ系列のDに手を出すのは悪手な気もするけど考え出す(この時点で40分)。
はじめの文字列は、AB。この後、AAの間には $c_{AA}$, ABの間には $c_{AB}$, BAの間には $c_{BA}$, BBの間には $c_{BB}$ を入れることができる( $c_{XX}$ は A か B のどちらか)。N文字になるまでこの操作を好きなだけやったときに、できる文字列の種類を答える問題。
もし、長さNの文字列が与えられたときに、操作を繰り返してその結果にできるかどうか、を考えてみる。どの操作で、どのような文字列が作れるかを考えてみる。特に、AとBの配置にどんな制限が出てくるかを考える。
まず $c_{AB}$ が A か B かで分けて考える。A の場合、とりあえず、AABは作れる。この後も、AAA…ABは作れる。 $c_{AA}$ が A だったら、この「Aがずっと続いて最後だけB」しか作れないので1通り。 $c_{AA}$ が B だったら、とりあえずBをところどころに入れることは可能(連続2個以上ができるかどうかはまだわからない)。

「AAAAAB」の「AA」の間に「B」が入れられるなら、「ABAAABAB」のようなものは作れる。ABの間はAなので、もし「BB」というようにBを連続で出したいなら、 $c_{BA}$ がBじゃないといけない。AならBがとびとびの配置だけ。BならBも好きなだけ出せる。
Bがとびとびでも、好きな場所に出せる場合でも、1文字目がA、最後の2文字がABであることは確定なので、他のN-3文字について考えればいい。そもそも、N=2のときもN=3のときも1通りなので、これらは即答えを返せばいい(コンテスト中はミスったけど)。
好きな場所に出せるなら、$2^{N-3}$ 通り。飛び飛びなら、dpを使ってやればいい。何番目までを見てるかと、Bを使ったかどうかの2つを持ちながら更新する。こうしてすべてのケースで答えが出る。
$c_{AB}$ がBのときも同じようにすればいい。けど、「同じように」をきちんと書けなくて何度もWAを出す。最終的にAC(提出 #18280472)。危ない、終了3分前だった。
Bに戻ったけど、結局わからず終了。解説を見たら、方針は間違ってなさそう。で、コードを見直したら、ミスっている箇所を発見。書き直してAC(提出 #18281891)。これができないってのはイマイチなんだよなぁ。
レートは前回比 -2で、1463。Dがとけてなかったらヤバかったな。