なかけんの競プロノート
🕒 2020/11/01 🔄 2021/06/14

ARC107感想戦

🏇

AtCoder Regular Contest 107 に参加しました。画像はコンテスト中に書いたメモです。

Aは、はじめ見たときはめんどくさそうな感じがしたけど、それぞれ独立してるから、 $\\dfrac{a(a+1)}{2}$ たちを掛ければいいことに気づく。今見たら、もっと簡単に書けるだろって気がするけど、焦ってイマイチなコードで提出（提出 #17750095）。この時点で3分。ちなみに、今、解きなおしてみた（提出 #17769178）。

Bは、 $N,K$ が与えられて、 $N$ 以下の正の整数を使って、 $a+b-c-d=K$ の組が何個あるか、数える問題。 $N$ が大きいので愚直に数えるのは無理だけど、 $a+b$ を固定したら何組あるかはわかるので、それを利用するといい感じ。

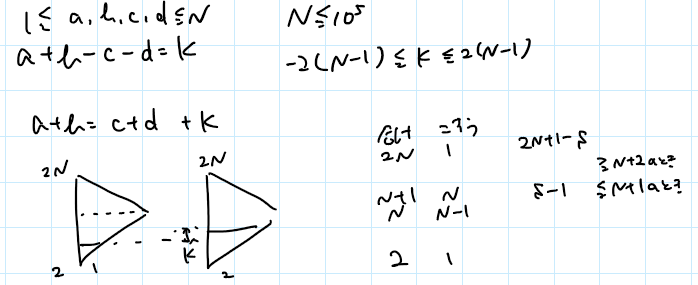
$a+b=c+d+K$ として、対称性があるから $K$ は0以上と考えてOK。 $a+b$ は $2$ 以上 $2N$ 以下の値しかとらず、 $a+b=2$ となる組は1通り、 $3$ となるのは2通り、…と増えていき、 $a+b=N+1$ となるのは $N$ 通りとなる。それより大きくなると、今度は1通りずつ減っていく。

なので、 $a+b=S$ となる組を考えると、 $S$ が $N+1$ 以下の場合は $S-1$ 通りで、 $N+2$ 以上の場合は $2N+1-S$ 通りとなる。 $c+d$ も同じ。

だから、 $a+b=S$ となる組の数と $c+d=S+K$ となる組の数（ $c+d=S-K$ の方を数えてもいい）を掛けて、 $S$ について足していけばOK。提出 #17752503。この時点で12分。

ここまでわりと順調そうな気がしたんだけど、勢いもここまで。Cを見て、難しそうだと思ってあまり考えずにDへ。Dのほうがおもしろそう。ということで考え始めたけど、ここが沼だった。

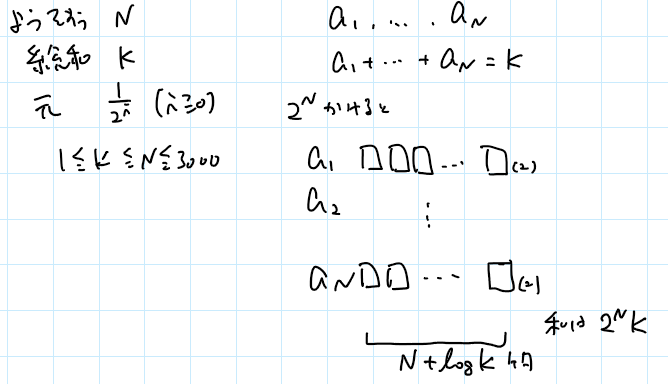
分数で考えるとめんどくさいから、 $2^N$ を掛けて考えてみればいっか。そうすると、それぞれの数は、2進数で表すと、 $N+\\log K$ 桁の数で和が $2^NK$ となるようにすればいいな、と。

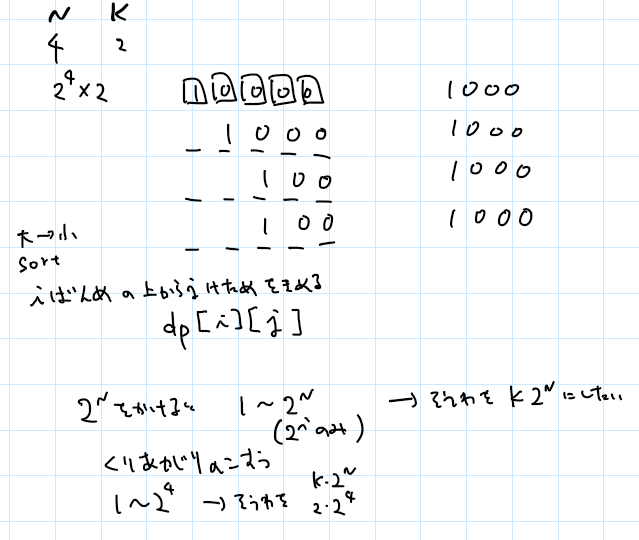
サンプルをもとに考えると、上の桁から考えていくのはどうだろうか。ただ、「何個の数を使ったか」「今どこの桁を見ているか」「（ $K2^N$ を作るために、今より後の数を使って）どれだけ繰上りが必要か」を管理しないとダメそうなので、間に合わない予感もしてくる。

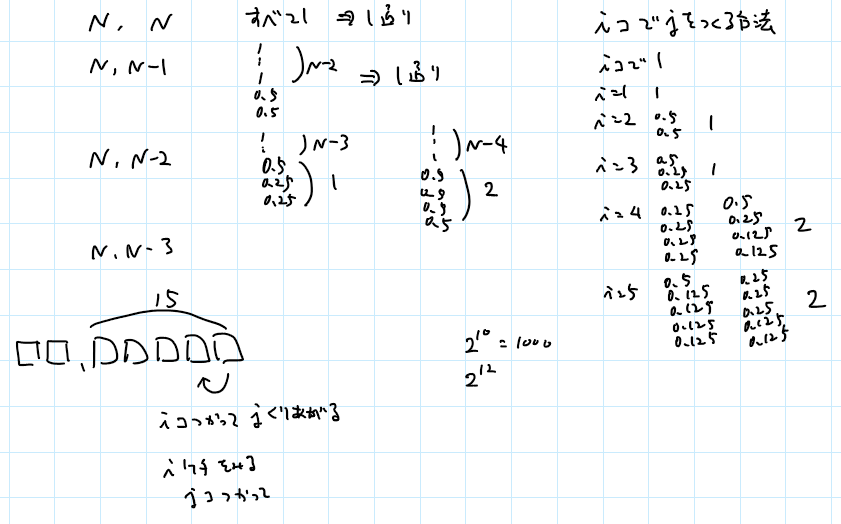
そのあと、方針を変えて、「 $K=N$ だったら、ぜんぶ $1$ のときしかないよな」と思って、 $K$ が大きい方から考えていくといいことがあるか？　と思って考えてみたけど、特に何も思いつかず。

左下のところでもう一度、桁に分けて考えてみたけど、よく考えれば $2^N$ を掛ける必要はなくて、小数点以下は15桁くらいしかありえないか、などと考えたりする（これはたぶん間違ってる）。まぁそんなこんなで解けないまま終了。

解説を見たら、Dはぜんぜん方針が違って、解説が頭良すぎ。でも、 $K$ が大きい方から考えたりしているときに、分割数みたいな考え方がひらめいていれば、解説のような考え方にたどりつくかもしれない。僕の実力では無理だったけど、絶対に思いつかないというレベルではないと思った。

あと、Cは、もっとちゃんと考えるべきだったな。Dが確実に解ける実力があるわけじゃないし、難易度的に、格闘していれば何とかなっていたかもしれない。

レートは少し下がった。このブログを始めてから、下がったってことしか書いていない気がするけど。。。