なかけんの競プロノート
🕒 2020/11/23 🔄 2021/06/14

ABC184感想戦

🐣

AtCoder Beginner Contest 184 に参加しました。画像はコンテスト中に書いたメモです。

Aは2x2の行列式を求める問題。定義式が書かれてるからそのまま答えるだけ。行列はもはや高校数学ではやらなくなったので、これを知ってるのは大学で数学をとった人か、機械学習とかを勉強してる人くらいかな。1分。

Bは、クイズの正解・不正解の結果が与えられるので、最終的な点数を答える問題。はじめはX点で、正解なら+1、不正解なら-1、ただし、点数はマイナスにはならない。これはそのまま言われたことをやるだけ。3分。

C。無限に広がる2次元グリッドがあって、ある場所からある場所へ移動するのにかかる最小移動回数を求める。斜めはどこまでもいける。また、上下左右合計3マスなら1回の移動で行ける。

なにこれ？ってなって、Dに向かう。

Dは、袋に、金貨A枚、銀貨B枚、銅貨C枚があって、1枚ランダムに選んで同じタイプの硬貨を1枚追加して2枚とも袋に返す、というのをどれかが100枚になるまで繰り返す。このとき、操作回数の期待値を答える問題。

操作ごとに1枚ずつ増えていくし、99/99/99のときは期待値1というのはわかる。でも、98/99/99以降どうすれば。。。式はわかるしDPを使うのはわかるけど、更新順序がわからない。。。Cへ戻る。

Cは、まず、1回で移動できるかどうかを判定する関数を作ってみる。

bool check(ll r1, ll c1, ll r2, ll c2) {
  bool ans = false;
  if (r1 + c1 == r2 + c2) ans = true;
  if (r1 - c1 == r2 - c2) ans = true;
  if (abs(r1 - r2) + abs(c1 - c2) <= 3) ans = true;
  return ans;
}

で、マスの和の偶奇が同じ場合は、斜めに動くのを2回やれば必ずたどりつける。だから、1回で行けなくて2回で行けるなら2回、と判定できる。

マスの和の偶奇が違う場合は、偶奇が同じになるように1回動いて、斜めに動くのを2回やれば、必ずスタートからゴールへは行ける。問題は、3回じゃなくて2回で行けてしまう場合をどうやって考えればいいか。

距離が3だけ離れたマスがやっかいなんだけど、

　スタート　⇔　スタートから3だけ離れたマス　⇔　ゴール

といけるかどうかを判定すればいい。これは、上の真ん中のセルに該当する場所それぞれに対して、スタートにもゴールにも行けるか、を考えればいい。

  ll ans = 3;
  if (r1 == r2 && c1 == c2) {
    ans = 0;
  } else if (check(r1, c1, r2, c2)) {
    ans = 1;
  } else {
    if ((r1 + c1) % 2 == (r2 + c2) % 2) ans = 2;
    for (ll i = -4; i < 5; i++) {
      for (ll j = -4; j < 5; j++) {
        ll r3 = r1 + i, c3 = c1 + j;
        if (check(r1, c1, r3, c3) && check(r2, c2, r3, c3)) ans = 2;
      }
    }
  }

普通に難しいんだが。ミスりまくりそうな予感はしたけど、一発で通って驚く。ここまでで23分。

Dに戻る。

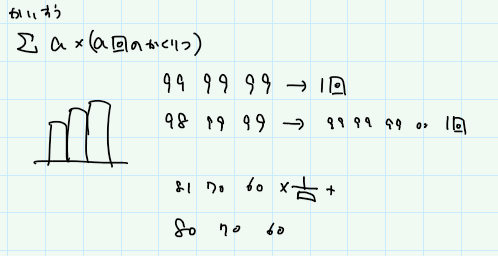
はじめ、回数がa回になる確率を出すのかなと思ってたけど、期待値をそのまま出せばOKというのに気づく。

X, Y, Z枚のコインがあるとき

  • 金が出て（1回）、X+1, Y, Z 枚の状態になる
  • 銀が出て（1回）、X, Y+1, Z 枚の状態になる
  • 銅が出て（1回）、X, Y, Z+1 枚の状態になる

の3つのケースがあるので、コインが多い場合から順番に考えていけばOK。ただ、更新の仕方がわからず、なかなかはまってしまった。だいぶ時間がかかったけど、AC（提出 #18331873）。ここまでで60分。あと1問やるには結構ギリギリ。

Eを見る。ワープ。。。前のPASTか。。。Fも見る。Nが40以下。半分全列挙でいけそうじゃん。こっちやろう。

N個の問題があって、各問題のかかる時間が $A_i$ 分とわかっている。 T 分以内に問題を解くとして、選んだ問題を解くのにかかる時間の和の最大値を答える問題。

Nは40以下なので、半分に分けて、和をそれぞれ全部計算してsetに入れておく。1つ目のsetから値を出して、和がTを超えないような値を2つ目のsetから出して計算していく。

方針はあっていたはずで、setでloewr_boundを使うときの注意にも気を付けた。

参考：std::lower_bound の罠について - えびちゃんの日記

が、サンプルが通らなくて、なんでだろうなんでだろうと迷走。なんだかよくわからない答えが返ってきて、なんでそんな答えが返ってくるんだろう、とか考えてたりした。とりあえず、記念提出したけれど、もちろんWA（提出 #18341005）。その後も、どこが間違っているのかわからず、時間終了。

コンテスト後、解説を見たらやはり方針はあってそう。なんでできなかったんだろうとよく見たら、lower_boundの使い方が間違っているじゃないか。。。1つ目のsetから取り出したtに対して、T-tを検索してたけど、これが原因。

2つ目のsetには、和にマイナスをつけてinsertする。で、t-Tを検索すれば、ちゃんとできた（提出 #18345306）。うーん、これはできておくべきだったなぁ。

順位から考えるともっと被害が大きいかと思ってたけど、それほどひどくはなかった。