なかけんの競プロノート
🕒 2020/11/09 🔄 2021/06/14

ABC182感想戦

🧦

AtCoder Beginner Contest 182 に参加しました。画像はコンテスト中に書いたメモです。

Aは、 $2A+100-B$ を返すだけだけど、 $B$ のほうが大きいこともあるかと思って、 $0$ との max を返してた。問題文を見れば、こんなことはする必要はないので、意味のないことをやっていた。ここまでで2分。

Bは、$A_1$ から $A_N$ の中で共通の約数を探したときに一番たくさん現れるものを答える問題。値は1000までしかないので、各値に対して、 $A_i$ を割り切ることができるかを数えていき、それらの最大を答えればいい。ここまでで4分。

Cは、各桁が0ではない数が与えられるので、いくつかの桁を除外して桁を詰め、3の倍数にできるかどうかを答える問題。3の倍数にできるなら、最小でいくつの桁を除外するかも答える。

直感的には、1個か2個はぶけばいいんでしょ、と思ったけど、最後のサンプルを見たらそれだとまずそう。なので、bit全探索しようという発想になってしまった。とりあえず全部書けばいいよね、と。

Cでこんなに時間のかかるものがあるはずない、と思いつつ、途中まで書いて、時間がかかりそうだからDを見る。うーん、こっちはこっちでめんどくさそう？

大人しくCに戻って、直感的に思いついた方法でやることにした。

3の倍数になるかどうかは、各桁の和が3の倍数になるかどうかだけを考えればいい。なので、まずは各桁を配列に入れる。で、例えば、「1234」だったら、1か4を除けばOK、みたいな考え方をしたいので、3で割ったときの余りが1である桁の数と、余りが2である桁の数も数えておく。

各桁の合計が3の倍数だったら、0を出して終わり。合計を3で割って1余ったら、「3で割って1余る桁を1つ削除」か「3で割って2余る桁を2つ削除」する。これでできれば、1か2を答える。どっちでやっても0になっちゃうなら-1と答える。合計を3で割ったときの余りが2のときも同様にやる。

提出したら、配列の書き方をミスっていてRE。再提出してAC（提出 #17965270）。ここまでで20分。あぁ、今回もレートが下がってしまう予感がする。

一瞬だけ見たDへ。 $A_1$ から $A_N$ を次のように足していく。はじめは1項目まで、次は、1項目から2項目まで、次は1項目から3項目まで。こうして最後まで足すと、 $N(N+1)/2$ 個の数を足すことになるけど、最初から答えを順番に見ていったときに、一番大きい値は何？　というもの。

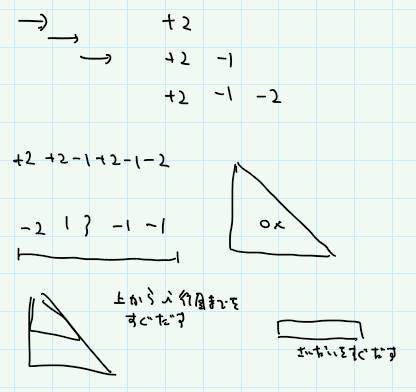
はじめはとりあえずサンプルを書いて見て考えてたけど、すぐには思いつけない。途中で最大になるなら、その次は大きなマイナスがあるのか？　とか思ったけど、もっと最後の方の計算で大逆転があったりするかもしれないから、この考え方はよくないな、と思い直した。

よく考えると、数字の並びは変わらないんだから、 $A_1$ から $A_i$ までを足していったときに、どこで最大になるかさえわかっていれば、答えがすぐに出せる。

添え字をバグらせずに書く自信はまったくなかったけど、一発でうまく書けた。あってるのかはよくわからないけどAC（提出 #17971978）。ここまでで33分。

Eは、ランプが照らせるマスを数える問題で、これはどこかで見た記憶がある。似たような問題がすでに出題されていたような？　まぁ気にせずやる。

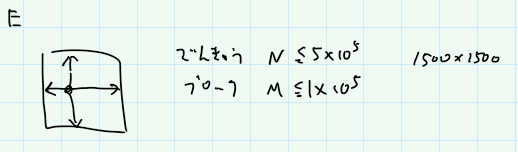
ほとんど何も考えてなくて、単純に各行、各列に対して、ランプがあったら伸ばす、ブロックがあったら止める、を4方向に対してみていけばOK。ランプを中心に考えるのではなく、セルを中心に考える。ランプの数とかはあまり関係なくて、セルの個数だけが重要。

既視感があったので何かの罠かと思い、時間も2秒じゃなくて2.5秒だったので、何かの罠かと思ったんだけど、無事にAC（提出 #17978768）。ここまでで51分。

CとかDでてこずったけど、Eがすんなりいったので、結構時間に余裕がある。Fはいつもできる気がしないんだけど、とりあえず考えるだけ考えてみる。

N種類のコインがあって、X円のものを買うために、数種類のコインを使って支払いをした。すると、おつりのコインは、渡したコインと同じ種類のものが1つもなかった（おつりがないケースも考える）。このとき、支払った金額としてあり得るものは何種類？　という問題（他にも条件はある）。

なるほど、意味が分からない。

とりあえず、 $y$ 円払うとする。払った金額y円と、おつり $y-X$ 円を考えた場合、それぞれを構成するコインは異なる。なので、 $A_i$ が $y$ で使われるか、 $y-X$ で使われるか、どちらでも使われないか、これら3つのうちのどれか1つだけが成り立つなぁ、というのはわかる。

さらに、 $y$ は $y-X$ より必ず大きい（おつりだから）ので、一番大きなコイン $A_N$ を使うとしたら、 $y$ の方しかない。しかし、その後はどうすれば。。。

いや、下から決めていくのか？ $A_1=1$ を使うとすれば、その次は $A_2$ を考えることになる。 $A_3$ たちが $A_2$ の倍数になることを使えば、全体を $A_2$ で割って、とかやるのか？

なんだか解けない気がしてきたけど、ちょっといきなり抽象的なケースで考えるのは大変だから、サンプルをもう一度考えてみることにする。

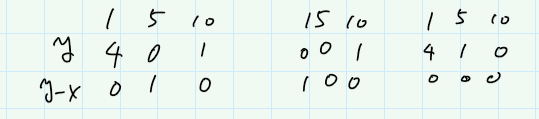
3種類コインがあって、9円のものを買う、と。で、もし10円玉を払ったなら、5円玉も払ったケース、払ってないケースの2つがありえる。もし10円玉を払ってないなら、5円玉を1枚払うケースがある（2枚払うのは、払う枚数が10円玉1枚より多いからダメ）。

で、こういうのをもとに、上から順番に決めていく方針で書いてみたらサンプルが通ったので提出してみる。TLE（提出 #17991198）。ただ、TLEしてるケースは１つだけ。なので、もう少し考えてみる。

上から順番に決めていけば、どんどん小さな金額をどうやって作るかを考えればいいので、小さい金額だけメモ化してみると通った（提出 #17992965）。ここまでで、99分16秒。ギリギリすぎる。

全完したので、気分がよかったんだけど、今Fのコードを見直してみたら、間違っているような。。。なぜこれでできているんだろう。というか、考え方がそもそも間違っている気がする。

喜んでいたけれど、これは本当の実力ではなさそう。。。