なかけんの競プロノート
🕒 2020/11/02 🔄 2021/06/14

ABC181感想戦

🏈

AtCoder Beginner Contest 181 に参加しました。画像はコンテスト中に書いたメモです。

Aは、 $N$ が偶数か奇数かで分けて答えればOK。1分。

Bは、 $0$ から $B_i$ までの和から、 $0$ から $A_i-1$ までの和を引けばOK。これらを $i$ について足せば答え。 $0$ から $n$ までの和は $\\dfrac{n(n+1)}{2}$ で出せるけど、最近よく見る気がする。この前のARCにも出てた。ここまでで3分。

Cは、3点が同一直線上にあるかどうかを判定する問題。傾きが一致しているかを考えればいい。

傾きは、 $y$ の増加量を $x$ の増加量で割ればいいけど、分母が $0$ だったら困るので、掛け算の形に直してからチェックする。ここまでで8分。

Dは、1から9までの数字からなる文字列 $S$ が与えられるので、並び替えて8の倍数が作れるか判定する問題。1000は8の倍数なので、結局下3桁だけで8の倍数かどうかは判定できる。

下3桁だけで考えると、8の倍数は高々125個。なので、3桁の8の倍数それぞれについて、与えられた $S$ から作れるかどうかを判定する。

例えば、512を作れるかどうかは、 $S$ の中に、 1, 2, 5 がそれぞれ1個以上ずつあれば作れる。 448 が作れるかどうかは、 4 が2個以上、8が1個以上あれば作れる。

なので、各数字が何個あるか数えて、8の倍数それぞれについて、各桁で使われている数字の個数を比較していけばいい。ただし、文字列に 0 がないので、 0 を含んでる物は作れない。

ここまではすぐに思いついたけど、2桁以下が少し問題。うーん、でも、各桁で使われている数字の個数を比較するときに、0 の個数は無視するようにすればOKかな。と思って提出したらWA（提出 #17794701）。

よく考えると、0の個数を無視するのはダメだった。例えば、 $S$ が 4 のときにYesになってしまう（40が作れると判定されてしまってた）。ということで、素直に $S$ の文字列の長さで分けることにする。

$S$ が3文字以上の場合は、先ほど書いた、各桁で使われている数字の個数を比較する方法でOK。0の個数も比較する（例えば、800とか200とかは作れないと判定されてほしい）。 $S$ が1文字の場合は、もちろん、8の場合だけがYes。問題は $S$ が2文字の場合。

$S$ が2文字の場合、3桁目が 0 なので、少し面倒なことになってしまう。ただ、96までの8の倍数が作れるかを同じように判定すればいいかと思って、提出したらWA（提出 #17797674）。

これ以上WAを増やすわけにはいかないと思って、もうなりふり構わず、2桁の場合は全部愚直に書いた。

これでようやくAC（提出 #17798629）。これでACじゃなかったらやばかった。ここまでで、29分。

ちなみに、2回目で提出したコードは、「0の個数を無視する」となっていたところが間違っていて、修正したらちゃんと通った（提出 #17829632）。

Eは、まぁとりあえずペアは、すぐ右か、すぐ左の人と組むのがよさそう。

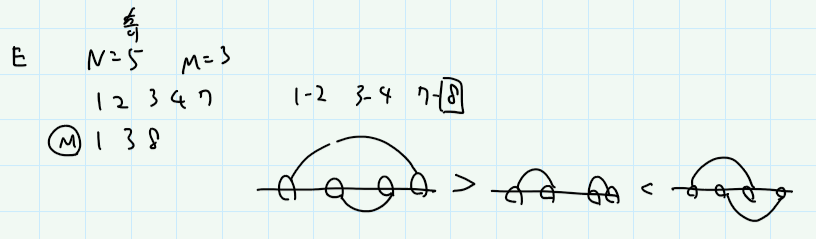
誰かをまたいじゃうときは、またがないようにした方が距離が近くなるので。なので、それぞれの人について、左の人との距離、右の人との距離を先に計算するとよいのかな？　などと思う。

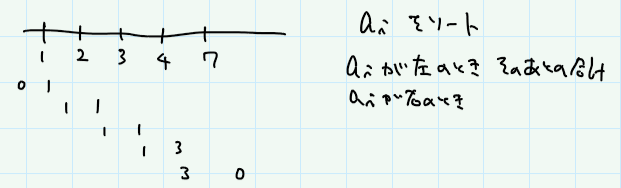
各変身について、和をはやく出さないといけない。和をはやく出すには累積和を使えばよさそう。

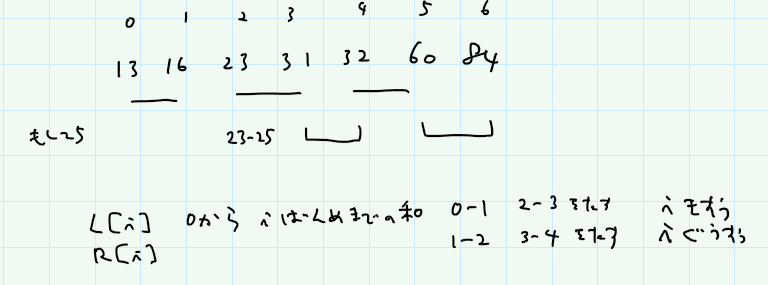
はじめを0番目として、「偶数番目-奇数番目」というペアを組んだ時に、i番目までの和を出すものと、「奇数番目-偶数番目」というペアを組んだ時に、i番目までの和をだすものとを計算しておく。より具体的にはこう書いておく。

  for (ll i = 1; i < N; i++) {
    if (i % 2 == 1) {
      L[i] = L[i - 1] + H[i] - H[i - 1];
      R[i] = R[i - 1];
    } else {
      L[i] = L[i - 1];
      R[i] = R[i - 1] + H[i] - H[i - 1];
    }
  }

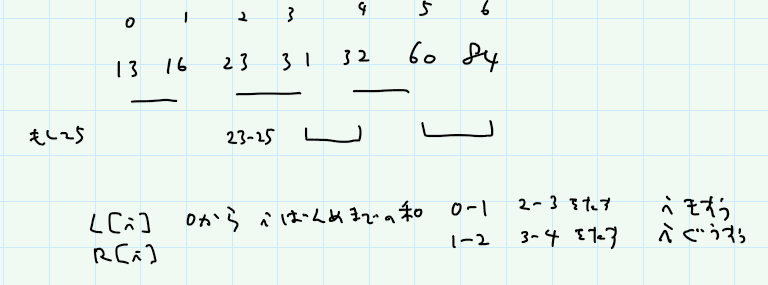
これを先に計算しておいて、例えばサンプル2の場合に、25を挿入したくなったらどうするかを考えてみる。この場合、3番目の前に入れることになる。wi = 3としておく。これより左の部分は、L[wi - 1]となる。先生を含むペアは w - H[wi - 1]で表せる。残りの右の部分は、R[N - 1] - R[wi]と書ける。この3つを足せば、身長の差の合計がすぐ出る。

wiが奇数の場合は上の通りだけど、偶数のときとか、左端、右端の場合はちょっと状況が違うので、それぞれ考えながら書いてみると、一発でサンプルが通って自分でも驚いた。こういうコードで、絶対に添え字とかを間違うのに。提出してみたらACだったのでさらに驚いた（提出 #17810111）。この時点で66分。

これが緑パフォか。つらいな。これ、通せる自信はまったくなかったんだけど。

もう時間がギリギリだけど、Fも一応見てみる。

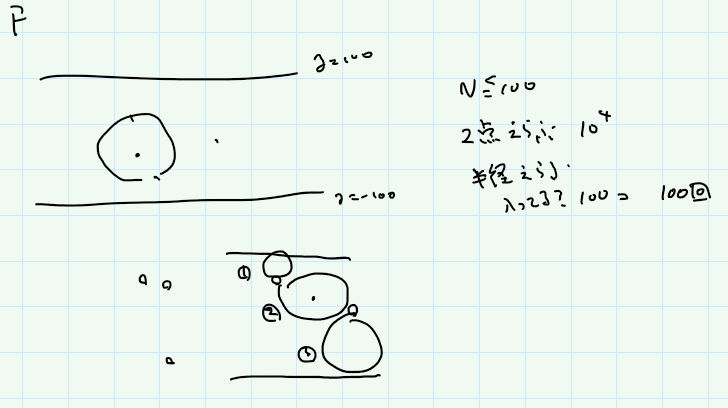
はじめ、2点を選んで、その中点を中心とする円を書いて、他の点を含んでたらダメ、っていう判定して二分探索すればいいのかと思ったけど、よく考えたらぜんぜん違ってた。別に円の中心が2点の中点を通るのが最適ではなくて、どっちかの点に寄りながら通ったほうが最適な場合もあるので。直線側を通るのが最適な場合もあるし。

ということで、何もできないままFは終了。終了後に解説を見たけど、うーん、これは思いつかない（提出 #17822396）。

失ったレートを考えると、まだまだ取り返すのに時間がかかるなぁ。。。