なかけんの競プロノート
🕒 2020/10/25 🔄 2021/06/14

ARC106感想戦

🦍

AtCoder Regular Contest 106 に参加しました。画像はコンテスト中に書いたメモです。

Aは、与えられた $N$ に対して、 $3^A+5^B=N$ が存在すれば求める問題。 $A, B$ の候補を全部確かめていけばOK。

でも、3を掛け続けたり、5を掛け続けたりしたときに、オーバーフローに気を付けないといけないな、と思う。で、前に見た、「オーバーフローしてないかどうかのチェックにdoubleを使う」っていうのをやってみた。が、あとで他のツイートを見て、そもそも1e18に5を掛けてもオーバーフローしないってのを見て、たしかにそうだと思った。間抜けだ。少し時間をロスした。この時点で5分。

Bは、操作をやっても総和が変わらないので、総和が等しいことが必要だとはすぐにわかったけど、それが十分なのかがわからず。

閉路がなかったら大丈夫そうだなという気はした。でも、閉路があると、操作をやっていったときに、最後の頂点でつじつまが合わなくなったりするかな？というのが自信なく。でも、閉路1個1個チェックしていくの大変そうだし、通してる人数を見ると、きっとこれで十分のはず、と未証明で「総和が一緒ならYes」で提出（提出 #17615740）。1WA。

なんでダメなんだ、やはり証明しないとダメか、と思ったけど、問題をよく見たら、Mが0のときもある、つまり、連結じゃないこともあるのか、と思って、なるほど、各連結成分での総和が一緒じゃないとダメなんだな、と思い直す。これで提出してダメならあきらめようと思って提出（提出 #17618911）。AC。AtCoderライブラリを使って、使い方を調べつつやったのもあって、この時点で23分。

今解説を見てみたら、木じゃないときは全域木を抜き出して考えればいいのか、なるほど、うーん、思いつけないのは頭が悪いな。

Cを見る。見るからにめんどくさそうだったので、Dも見る。これは形式的冪級数ってやつか？無理。仕方なくCにいく。

とりあえず、サンプルを理解する。文章は長いけど、大して難しいことはやってないな、と思って気分を落ち着かせる。

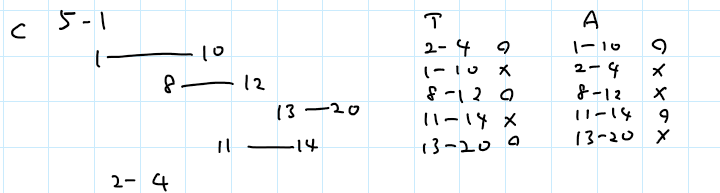
で、とりあえず、取り得る値を考える。T-A=Mの式で、少なくともTもAも1以上だから、MがNになることはないな、などというのを考える。で、そもそもA=1のときを考えると、Aで選んだ1個の区間は他の全部の区間とそれぞれ交わってるから、Tは最大でもN-1しか無理だな、というのもわかる。なので、Mは、N-2以下しかありえない。

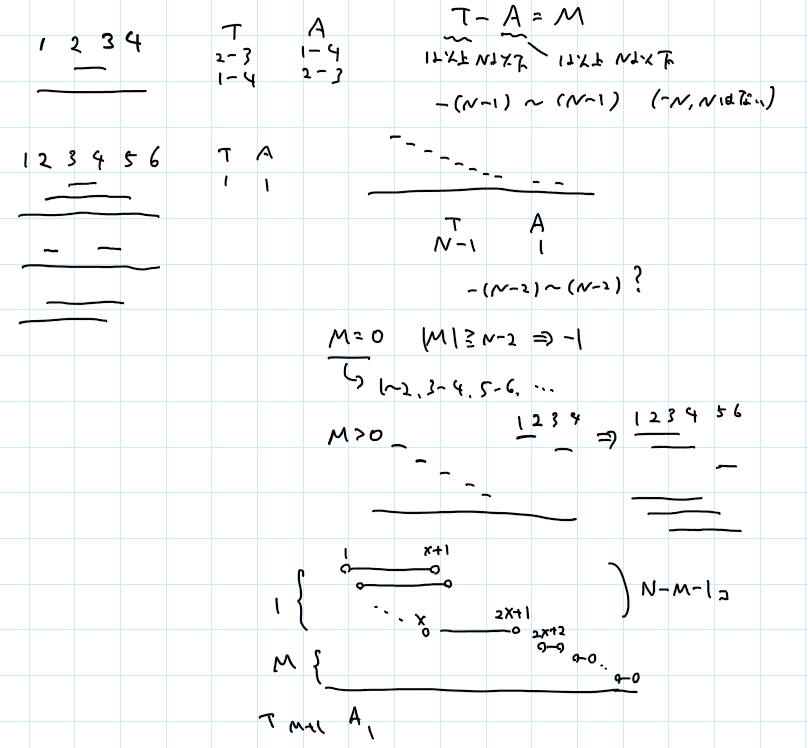
で、T=N-1で、A=1となるときを考えると、1-1e9の区間と2-3、4-5、6-7、…の区間を考えればいいことがわかる。左でソートすると、めちゃデカ区間をいきなり選ぶからA=1、右でソートすると、めちゃデカ区間が最後で他は全部選ぶからOK。

Mが正のケースでは、先ほどの答えを利用して、T=M+1、A=1となるようにする。M個の互いに交わってない区間、めちゃデカ区間、互いにぜんぶ交わっている区間（N-M-1個）とやれば、うまくいくじゃん。天才。

M=0はT=N、A=Nとなるようにすればよくて、Mが負の場合は、上の答えを逆順にすればいっか、と安易に思ったんだけど、よく考えるとうまくいかないことにきづく。あれ、これどうすればいいんだ？と少し戸惑う。で、冷静にもう一回考える。

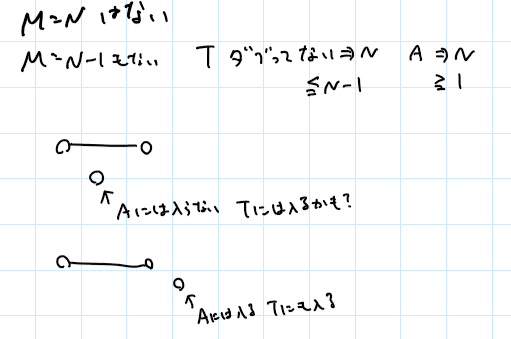
M=N,N-1がないことを確認、Mが正のときもとりあえず再確認、で、Mが負になる場合を考える。左端でソートしたとき、ある区間を採用したとき、次の区間が交わってたらAには絶対はいらないがTには入るかもしれない。次の区間が交わってなければAには入るがTにも入る。なるほど、負になる場合はないんだな。

解説を見たら、Tの解法はスケジューリング問題の最適解を求めるものだから、Mは負にならない、と。なるほど、それはそう。

で、ここまでの内容をコードに書いて提出（提出 #17629371）。WA。明らかに間違っていたところを直して提出しても、まだWA。なんでや。

1つだけ通らなかったので、どんなコーナーケースがあるかなと思って制約をよく見たら、N=1もあるのか。なるほど。「M=N,N-1はない」と思っていたけど、N=1のときは、M=N-1のケースがあるのか。厳しい。再提出（提出 #17631321）。AC。この時点で、72分。

とりあえず、Dも見るけど、これって形式的冪級数っていうやつ、使うんでしょ？どうせきっと無理だよ、と思いつつ、考えてみる。

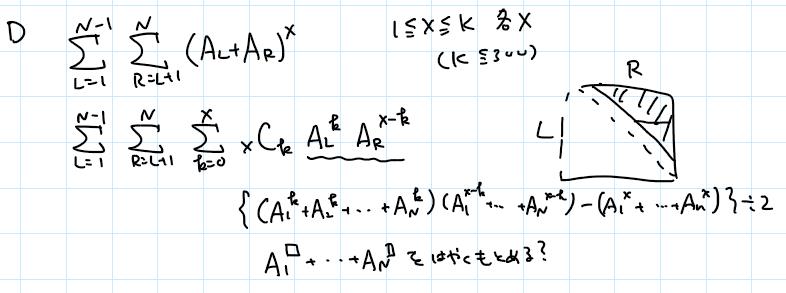
あれ？　これ、二項定理使って展開しただけでうまくいきそう。積の和を速く計算すればいいのか。積の和は、k乗の和が速く計算できればいいから、これ実はそんなに難しくないかも。しかし、今までのロスで、時間がない。間に合うかわからんけど書く。が、結局バグがとれず、記念に提出だけする（提出 #17636645）。

コンテスト終了後も格闘して、二項係数を計算する自分のライブラリがおかしかったこと、modのとり方がおかしい、配列の添え字がおかしい、などのバグがあって、それらをクリアしたら通った（提出 #17638835）。これは頑張れば通せてたかもしれないけど、残り30分の状態で考えてコードを書くところまで仕上げるのは無理だったので、なかなか厳しいものがある。ABCのFよりもやさしかったな。

今までの低下を補うのに何年かかるペースなんだ。。。