なかけんの競プロノート
🕒 2020/10/04 🔄 2021/06/14

ARC104感想戦

🗾

AtCoder Regular Contest 104参加しました。

というわけで、NoSub方針で行ってたんですけどね。

まず、Aを見ると、たしかにABCのAと同じレベルでしたね。で、B以降をチラ見して、ちょっとCを考えてみようかなとしてみました。

以下は、考えたときのメモと考えていた内容。

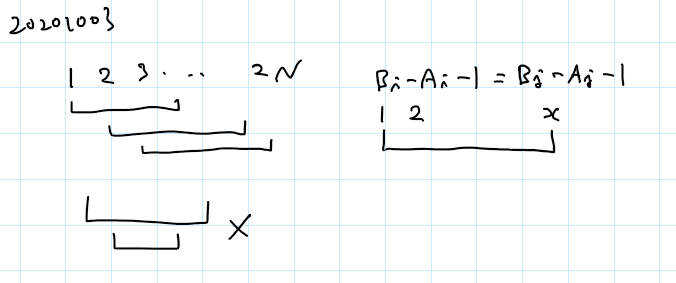
問題文の意味は分かるけど、どうするかはまったくわからず。とりあえず、ある範囲が別の範囲に含まれてしまうケースはないんだなと思ったけど、だから何？という感じ。-1の処理がまったくわからない。。。

で、Dを見てみると、まだこっちのほうが考えやすそう。

はじめは、i番目まで見て、j個数字を使ったときに、和がkになる作り方を計算していけば一応答えは出そうだと思いました。でも、それだとkがでかすぎる（上では10000って書いてるけど、これは間違いで、実際はもっと大きい）。

で、「平均がxになるって、なんか別の考え方があったような？」って考えて思い出したのが右下のやつです。はじめからxを引いて、和が0になるような場合を考えればいい、と。そうすれば、何個の数字を使うか、という個数が無視できます。

x未満のやつは負で、xを超えてるやつは正なので、和が同じになるものを数えればいい、と考えました。例えば、左側の和が-5になるのが2通りで、右側の和が5になるものが3通りだったら、-5+5とできる方法が6通りあるということです。さらに、xは何個使ってもいいので、1+K倍すれば解けそう。結局、和が〇になる場合の数を事前に求められればいいんだな、とは思っていました。

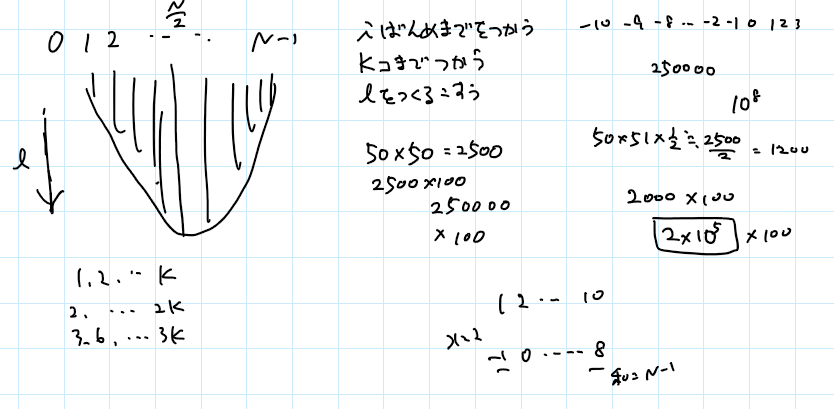
i番目までの数字を使って、和がlになる場合の数を考えようとしていました。時間が厳しそうなのと空間も厳しそうな気がしていました。よく考えると、例えば、平均が2の場合は、「1までを使って和がlになる場合の数」と「N-2までを使って和がlになる場合の数」を掛け合わせていけばいいのですが、前者は最大でもKにしかならないので、場合の数を考えるときにlは最後まで考えなくてもいい、ということはわかりました。

この時点で、どっちかというと空間の制限のほうが心配になってきました。配列のサイズってどれくらいまでいけるんだっけ？と。で、バッファー込みで2*10^5×100のサイズはコードテストでも問題なく作れそうなことがわかりました。vectorは時間がかかるので、配列で。

で、サンプルが通ったので時間の制限をあんまり意識しないまま提出して、TLE（提出 #17173803）。その後も、いろいろいじってドツボにはまってしまいました。残り時間も無くなってきたので、とりあえずAだけ解いて終了。ツイート通りの展開でした。

まぁそうなりますよね。

D、解説を見たけど、mod iごとにスライドしながら和をとるのか、たしかに言われたらそうなんだけど、思いつかなかったなぁ。K個の和を考えるのに毎回K回計算しなくてもいいのかぁ。うーん。

だいぶレートが下がったので、また地道に上げていきます。