AtCoder AGC 039 D - Incenters (1000点) 解説
問題
問題文は本家サイトにあります:AtCoder AGC 039 D
問題概要
3以上の整数 $N,L$ と、項数が $N$ の数列 $\{T_i\}$ が与えられる。
$xy$ 平面上で、原点を中心とする円周上に $N$ 個の点がある。 $i$ 個目の点の座標は $\left(\cos\dfrac{2\pi T_i}{L},\ \sin\dfrac{2\pi T_i}{L}\right)$ である。
これら $N$ 個の点から異なる3点を一様ランダムに選ぶとき、選んだ3点を頂点とする三角形の内接円の中心の $x$ 座標、 $y$ 座標の期待値をそれぞれ答えなさい。
制約
$3\leqq N \leqq 3000$
$N \leqq L \leqq 10^9$
$0\leqq T_i \leqq L$
$T_i\lt T_{i+1}$
入力はすべて整数
解説
本家サイトに解説がある(PDF) ので、ここでは、解説の解説をします。アルゴリズムはあまり関係なくて、ほとんど数学の問題です。
「3点から内接円の中心の座標を求める」というのがすでに難しいですが、3点の情報を使ってうまく表さないと計算が終わりません。 $N=3000$ なので、 $\mathcal{O}(N^3)$ だと計算が間に合いません。なので、計算量を落とすために、図形的な性質を使っていく必要があります。
さて、問題文にある $i$ 個目の点の座標 $\left(\cos\dfrac{2\pi T_i}{L},\ \sin\dfrac{2\pi T_i}{L}\right)$ を見てみます。これは、円周を $L$ 等分したあと、 $(1,0)$ から反時計回りに $T_i$ 個目の点(スタートを0個目と数える)を指していることになります(参考:【基本】三角関数の定義、【基本】弧度法)。下の図は、問題の例にある、8分割をして 1, 3, 5, 6 番目を選んだときの図です。
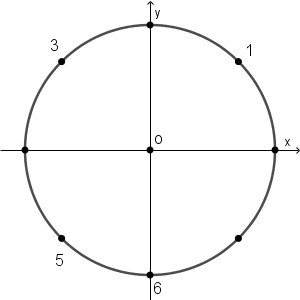
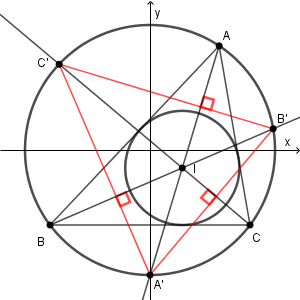
さて、では、内接円をどう考えていけばいいかを見ていきます。内接円とは、三角形の内側で接する円です。次のように、円周上の3点 A, B, C を結んで三角形を作り、内接円をかいてみます。
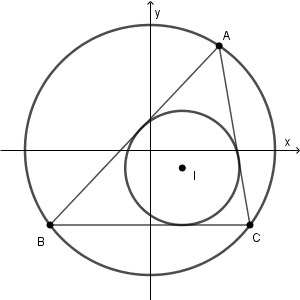
内側の円が内接円で、点 I が内接円の中心(内心といいます)です。内接円の性質はいくつかあります。一つは、内心は、それぞれの角の二等分線上にある、ということです。各頂点を I と結んでみます。
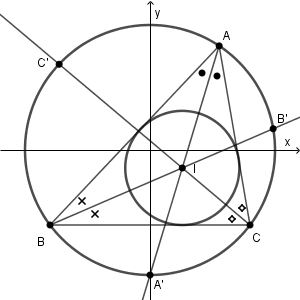
どうしてそれぞれの角の二等分線上にあるかは、【標準】三角比と内接円の上側にある図を参考にしてみてください。接点と頂点と内心を結んでできる三角形が合同であることを利用するとわかります。
3点 A, B, C が同一円周上の円であることを利用して、円周角の定理を使います。同じ長さの弧に対する円周角は等しく、逆も成り立ちます。なので、 AI と弧 BC との交点を $\mathrm{A'}$ と置くと、 $\mathrm{A'}$ は弧 BC のちょうど中間にあることがわかります。 $\mathrm{B'}$, $\mathrm{C'}$ についても同様です。
さらに、 $\mathrm{AA'}$ と $\mathrm{B'C'}$ との交点を D とおいて、もう一度円周角の定理を使ってみます。
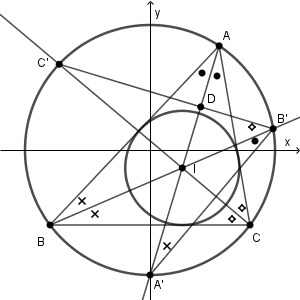
弧 $\mathrm{A'B}$ に対する円周角は等しいので、 $\mathrm{ \angle BAA'=\angle BB'A' }$ となります(黒丸の部分)。同様に、×と◇も等しいことがわかります。ここで、三角形 $\mathrm{ A'B'D }$ を見てみましょう。内角には、●と×と◇が1つずつありますが、これは三角形 ABC の内角の和の半分なので合計すると90度であることがわかります。つまり、 $\angle \mathrm{A'DB}'=90^{\circ}$ であることがわかります。
これは、 $\mathrm{ IA' }$ と $\mathrm{ B'C' }$ が垂直に交わることを示しています。同様にすれば、 $\mathrm{ IB' }$ と $\mathrm{ C'A' }$ が垂直に交わることも、 $\mathrm{ IC' }$ と $\mathrm{ A'B' }$ が垂直に交わることも示せます。つまり、三角形 ABC の内心は、三角形 $\mathrm{ A'B'C' }$ の垂心(各頂点から対辺に下した垂線の交点)に一致する、ということがわかります。
だいぶ長かったですね。しかし残念ながらこれはまだ本家サイトの解説の2行目に来ただけです。まだ1/3くらいしか終わっていません。
さて、今わかったのは、三角形 ABC の内心の座標を求めるには、各弧の中心を結んでできる三角形 $\mathrm{ A'B'C' }$ の垂心の座標を求めればいい、ということです。が、まったく簡単になった気がしません。ただ、本家サイトの解説にもありますが、外心、重心、垂心にはいい性質があります。オイラー線と呼ばれるものですが、これについて見ていきます。
外心というのは、外接円の中心のことです。外接円とは三角形の外で接する円のことです。上の図では、三角形 ABC の外心は原点です。原点を中心とする円周上の点をとる、ということは、その円周上の3点から作った三角形の外心は、自動的に原点になります。わかりやすいですね。また、三角形 $\mathrm{ A'B'C' }$ の外心も原点になることがわかります。
次に、重心です。これは、頂点と対辺の中心とを結んだ直線(中線といいます)を3本引いたときにできる交点のことです。重心は、中線を $2:1$ に分けることが知られており、座標は、各頂点の座標を足して3で割ったものになります。なお、重心が中線を $2:1$ に内分することは、【基本】三角形の重心に書いており、重心の座標の求め方は、【標準】三角形の重心の座標に書いています。
この外心と重心を使って、垂心を求めるには次のように行います。一般的な話をするので、先ほどとは別の名前を使いましょう。三角形 PQR に対して、この外心を O、垂心を H としましょう。
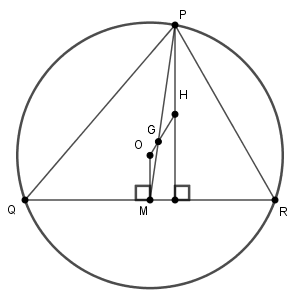
外心 O から辺 QR に垂線をおろし、交点を M とします。このとき、PH も QR とは垂直なので、 OM と PH は平行です。 PM と OH の交点を G とすると、三角形 GMO と三角形 GPH が相似であることがわかります。
次に、 OM と PH の長さを調べるために、別の角度から図形を見てみます。 R を通り QR に垂直な直線と OQ との交点を S とおきます。このとき、三角形 QOM と三角形 QSR は相似で、 M は QR の中点なので、 SR は OM の2倍になります。
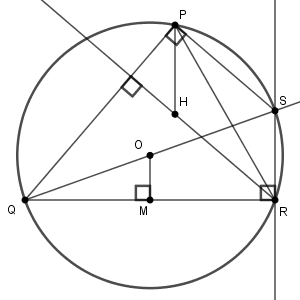
また、 SQ は直径となるので、 SP と PQ は垂直に交わります(直径に対する円周角は90度だから)。 HR と PQ も垂直に交わるため、 PS と HR は平行です。また、 PH と OM, OM と SR も平行だから、 PH と SR も平行です。
以上から、四角形 PHRS は平行四辺形だから、 $\mathrm{ PH=SR=2OM }$ であることがわかります。

以上から、三角形 GMO と三角形 GPH の相似比は $1:2$ であることから、 G が線分 MP を $1:2$ に内分する点であることがわかるので、 G は、実は三角形 PQR の重心であることがわかります。
まとめると、三角形 PQR の外心 O, 重心 G, 垂心 H は、この順番に一直線上にあり、 $\mathrm{ OG:GH }=1:2$ であることがわかります。この3点を通る直線のことをオイラー線といいます。
厳密には、 O が QR 上にあるときはどうするんだとか、他のケースも考えないといけませんが、このオイラー線のことが成り立つとして、問題に戻りましょう。このオイラー線のことを利用すれば何が言えるかを確認します。
円周上の3点 A, B, C をとって、三角形 ABC の内心を考えていたのでした。弧 BC, CA, AB の中点をそれぞれ $\mathrm{ A', B', C' }$ とすると、三角形 ABC の内心は、三角形 $\mathrm{ A'B'C' }$ の垂心と一致するのでした。
三角形 $\mathrm{ A'B'C' }$ も、外心が原点であり、重心は、各頂点の座標の和を3で割ったもので求められるので、オイラー線の性質から、垂心の座標は、各頂点の座標の和で求められることがわかりました(ここで、本家サイトの解説の第1段落が終了)。
さて、あとは足すだけですが、足し方も考えなくてはいけません。各三角形 ABC ごとに、対応する三角形 $\mathrm{ A'B'C' }$ を考えて、各頂点の座標を足す、とすると、結局3重ループになってしまいます。しかも\[ \sum_{i=0}^{N-3} \sum_{j=i+1}^{N-2} \sum_{k=j+1}^{N-1} (\mathrm{ A'+B'+C' }) \]のような形になり、足しにくいです。
しかし、 $\mathrm{A'}$ の座標が足されるのがいつか、で分類してみると、ループが減り、足すのも楽になります。 $\mathrm{A'}$ は点 B, C が決まると定まるので、 B, C が固定されたとして考えてみます。一つの辺が固定された、と考えます。この両端を、 $i,j$ 番目の点としましょう。 $i\lt j$ とします。
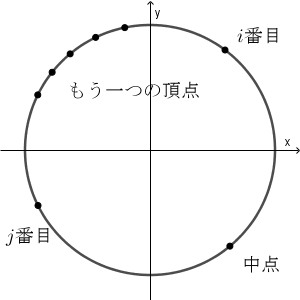
三角形のもう一つの頂点が上のような位置にあったとき、つまり、 $i, j$ 番目の間にあった時は、弧の中点は $i,j$ の中間の角に180度足したものになります。このような状況になるのは、 $j-1-i$ 通りあります。
一方、次のような位置関係のときもあり得ます。
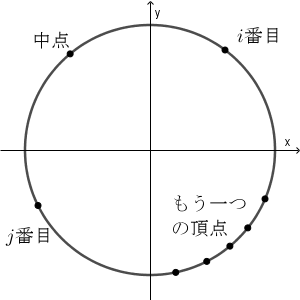
$i,j$ の間にないときです。このとき、弧の中点は、 $i,j$ の中間の角になります。このような状況になるのは、先ほど見たケースと $i, j$ の点を除いたときなので、 $N - 2-(j-1-i)$ 通りとなります。
これ以外で $i,j$ の弧の中点の座標が足されることはないため、 $i\lt j$ の範囲で足し合わせていきます。期待値を求めるので、全体の三角形の選び方 ${}_N \mathrm{C}_3$ で割れば答えとなります。